Hai nguồn nhiệt đặt cách nhau s mét một nguồn có cường độ a đặt ở điểm A

Giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Bài 1.18 trang 15 SBT Toán 12 Tập 1: Hai nguồn nhiệt đặt cách nhau s mét, một nguồn có cường độ a đặt ở điểm A và một nguồn có cường độ b đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức

$I = \frac{a}{x^{2}} + \frac{b}{{(s - x)}^{2}}$

trong đó x (m) là khoảng cách giữa P và A. Tại điểm nào nằm giữa A và B nhiệt độ sẽ thấp nhất?

Lời giải:

Xét hàm số: $I = \frac{a}{x^{2}} + \frac{b}{{(s - x)}^{2}}$ , 0 < x < s.

Ta có: I' = $- \frac{2 a}{x^{3}} + \frac{2 b}{(s - z)} = \frac{2 [{bx}^{3} - a {(s - x)}^{3}]}{x^{3} {(s - x)}^{3}}$ , 0 < x < s.

Do đó: I' = 0 ⇔ $\frac{x}{s - x} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}}$ ⇔ x = $\frac{s \sqrt[3]{a}}{\sqrt[3]{a} + \sqrt[3]{b}}$ .

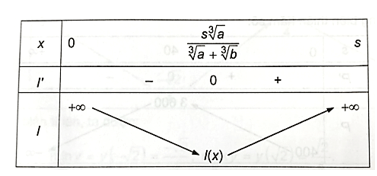
Ta có bảng biến thiên như sau:

Hai nguồn nhiệt đặt cách nhau s mét một nguồn có cường độ a đặt ở điểm A

Vậy tại điểm P trên AB và cách A một khoảng PA = x = $\frac{s \sqrt[3]{a}}{\sqrt[3]{a} + \sqrt[3]{b}}$ (m) thì nhiệt độ thấp nhất.

Lời giải Sách bài tập Toán lớp 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

SBT Toán 12 Kết nối

Hai nguồn nhiệt đặt cách nhau s mét một nguồn có cường độ a đặt ở điểm A

Giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Xem thêm các bài giải sách bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác: