Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích 300 cm^2

---

Giải sách bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Kết nối tri thức

Bài 1.36 trang 26 SBT Toán 12 Tập 1: Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích 300 cm², lề trái và lề phải là 2 cm, lề trên và lề dưới là 3 cm. Gọi x (cm) là chiều rộng của tờ giấy.

a) Tính diện tích của tờ giấy theo x.

b) Kí hiệu diện tích tờ giấy là S(x). Khảo sát sự biến thiên của hàm số y = S(x).

c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.

Lời giải:

Theo đề, ta có: x (cm) là chiều rộng tờ giấy.

Gọi y (cm) là chiều dài tờ giấy.

Theo giả thiết, ta có: chiều rộng vùng in là: x – 2.2 = x – 4 (cm).

                                  Chiều dài cùng in là: y – 3.2 = y – 6 (cm).

Diện tích vùng in là: (x – 4)(y – 6) = 300.

Suy ra y = $6+\frac{300}{x-4}=\frac{6x+276}{x-4}$ .

a) Diện tích của tờ giấy được thiết kế là:

S(x) = xy = $\frac{x\left(6x+276\right)}{x-4}$ .

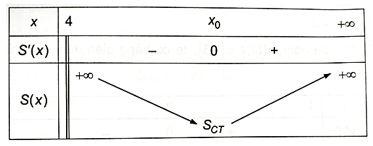
b) Khảo sát sự biến thiên của hàm số S(x): 

1. Tập xác định: D = (4; +∞).

2. Sự biến thiên

Giới hạn vô cực và giới hạn tại vô cực: $\underset{x\to 4^{+}}{\lim }S\left(x\right)=+\infty$ , $\underset{x\to +\infty }{\lim }S\left(x\right)=+\infty$

Ta có: S(x) = 6x + 300 + $\frac{1200}{x-4}$ .

S'(x) = $\frac{6{\left(x-4\right)}^2-1200}{{\left(x-4\right)}^2}$  .

S'(x) = 0 ⇔ x₀ = x = 4 + 10$\sqrt{2}$ .

Ta có bảng biến thiên như sau:

c) Kích thước của tờ giấy để nguyên liệu sử dụng ít nhất là khi chiều rộng x = 4 + 10$\sqrt{2}$ .

Khi đó chiều dài y = 6 + $\frac{300}{x-4}$  = 6 + $\frac{300}{4+10\sqrt{2}-4}$  = 6 +15$\sqrt{2}$ .

Vậy kích thước của tờ giấy để nguyên liệu sử dụng ít nhất là chiều rộng bằng 4 + 10$\sqrt{2}$  cm, chiều dài bằng 6 + 15$\sqrt{2}$  cm.

Lời giải Sách bài tập Toán lớp 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác:

• Bài 1.31 trang 25 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: ....

• Bài 1.32 trang 25 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: ....

• Bài 1.33 trang 25 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: ....

• Bài 1.34 trang 25 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm f'(x) xác định trên ℝ và f'(x) có đồ thị như hình vẽ sau: ....

• Bài 1.35 trang 25 SBT Toán 12 Tập 1: Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 ....

• Bài 1.37 trang 26 SBT Toán 12 Tập 1: Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x² + 10x + 5(triệu đồng) ....

• Bài 1.38 trang 26 SBT Toán 12 Tập 1: Cho điểm A(3;2 ) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B ....

• Bài 1.39 trang 26 SBT Toán 12 Tập 1: Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có 80 000 con ....

• Bài 1.40 trang 27 SBT Toán 12 Tập 1: Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài ....