Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x^2 + 10x + 5
Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị sản phẩm là
Giải sách bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Kết nối tri thức
Bài 1.37 trang 26 SBT Toán 12 Tập 1: Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x2 + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị sản phẩm là
a) Khảo sát sự biến thiên của hàm số y = f(x).
b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?
Lời giải:
a) Ta có: = 0,2x + 10 + với x ≥ 1.
f'(x) = 0,2 –
f'(x) = 0 ⇔ 0,2 – = 0 ⇔ x = 5 (do x ≥ 1).
Giới hạn tại vô cực: .
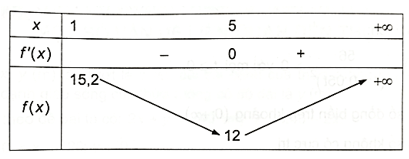
Ta có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng (5; +∞), nghịch biến trên khoảng (1; 5).
Hàm số đạt cực đại tại x = 5 với fCT = 12.
Lời giải Sách bài tập Toán lớp 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác: