Dùng bốn số: 0; 2; 3; 5 để tạo ra các số có bốn chữ số, mỗi chữ số đã cho chỉ lấy một lần sao cho

---

Giải sách bài tập Toán lớp 6 Bài 9: Dấu hiệu chia hết

Bài 2.18 trang 34 sách bài tập Toán lớp 6 Tập 1 - Kết nối tri thức với cuộc sống:

Dùng bốn số: 0; 2; 3; 5 để tạo ra các số có bốn chữ số, mỗi chữ số đã cho chỉ lấy một lần sao cho:

a) Các số đó chia hết cho 2

b) Các số đó chia hết cho 5

c) Các số đó chia hết cho cả 2 và 5.

Lời giải:

Gọi số có bốn chữ số cần tìm l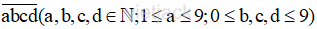à và 

Vì để tạo ra các số có bốn chữ số thỏa mãn yêu cầu đề bài nên a, b, c, d ∈ { 0; 2; 3; 5}

Vì mỗi chữ số đã cho chỉ lấy 1 lần từ 4 chữ số 0; 2; 3; 5 nên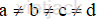

a) Để số đó chia hết cho 2 nên số đó có chữ số tận cùng là 0; 2; 4; 6; 8. 

Do đó d = 0 hoặc d = 2

+) Với d = 0, ta được các số: 5 320; 5 230; 3 520; 3 250; 2 530; 2 350.

+) Với d = 2, a khác 0 ta được các số: 5 302; 5 032; 3 502; 3 052

Vậy các số chia hết cho 2 là 5 320; 5 230; 3 520; 3 250; 2 530; 2 350; 5 302; 5 032; 

3 502; 3 052.

b) Để số đó chia hết cho 5 nên số đó có chữ số tận cùng là 0 hoặc 5. 

Do đó d = 0 hoặc d = 5

+) Với d = 0, ta được các số: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230

+) Với d = 5, a khác 0 ta được các số: 3 025; 3 205; 2 035; 2 305.

Vậy các số chia hết cho 5 là: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230; 3 025; 3 205; 2 035; 2 305.

c) Để số đó chia hết cho cả 2 và 5 nên số đó phải có chữ số tận cùng là 0. Do đó d = 0

Với d = 0 ta được các số: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230

Vậy các số chia hết cho cả 2 và 5 là 3 520; 3 250; 2 530; 2 350; 5 320; 5 230.