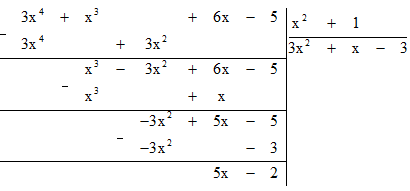Cho hai đa thức A = 3x^4 + x^3 + 6x −5 và B = x^2 + 1

Cho hai đa thức A = 3x + x + 6x −5 và B = x + 1. Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.

Giải SBT Toán 7 Kết nối tri thức Bài 28: Phép chia đa thức một biến

Bài 7.29 trang 34 sách bài tập Toán lớp 7 Tập 2: Cho hai đa thức A = 3x⁴ + x³ + 6x −5 và B = x² + 1. Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.

Lời giải:

Thực hiện phép chia (3x⁴ + x³ + 6x −5) : (x² + 1)

Vậy phép chia (3x⁴ + x³ + 6x −5) : (x² + 1) có thương Q = 3x² + x − 3 và dư R = 5x − 2

Kiểm nghiệm BQ + R = (x² + 1)(3x² + x − 3) + 5x − 2

= x²( 3x² + x − 3) + 1. (3x² + x − 3) + 5x − 2

= 3x⁴ + x³− 3x² + 3x² + x − 3 + 5x − 2

= 3x⁴ + x³+ (−3x² + 3x²) + (x + 5x) + (−3 − 2)

= 3x⁴ + x³ + 6x −5 = A