Cho M là một điểm tùy ý bên trong tam giác đều ABC
Giải SBT Toán 7 Ôn tập chương 9
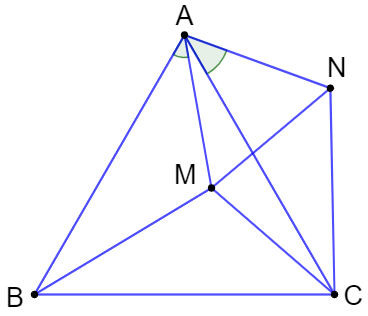
Bài 9.24 trang 60 sách bài tập Toán lớp 7 Tập 2: Cho M là một điểm tùy ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho và AN = AM. Chứng minh:
a) Tam giác AMN là tam giác đều;
b) ΔMAB = ΔNAC;
c) MN = MA, NC = MB.
Lời giải:
a) Ta có: (do tam giác ABC đều).
Lại có: AM = AN nên suy ra tam giác AMN cân tại A.
Vậy tam giác AMN là tam giác đều.
b) Tam giác ABC đều nên suy ra AB = AC.
Xét ∆MAB và ∆NAC có:
AB = AC (cmt)
AM = AN (gt)
(gt)
Do đó ∆MAB = ∆NAC (c.g.c)
c) Vì tam giác AMN đều (cmt) nên MN = MA.
Do ∆MAB = ∆NAC nên MB = NC (hai cạnh tương ứng).