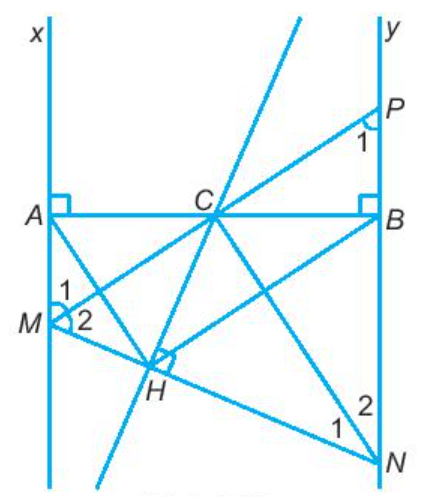
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng

Giải SBT Toán 7 Ôn tập chương 9

Bài 9.26 trang 60 sách bài tập Toán lớp 7 Tập 2: Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN. Chứng minh:

a) AM + BN = MN;

b) CM là đường trung trực của AH, CN là đường trung trực của BH;

c) Góc AHB là góc vuông.

Lời giải:

a) Xét ΔAMC và ΔBPC có:

AC = CB (gt)

$\widehat{MAC}=\widehat{PBC}\left(=90°\right)$

$\widehat{ACM}=\widehat{BCP}$(hai góc đối đỉnh)

Do đó ΔAMC = ΔBPC (g.c.g)

Suy ra MC = CP (hai cạnh tương ứng).

Mà NC ⏊ MP.

Suy ra NC là đường trung trực của MP.

Vậy nên tam giác NMP cân tại N.

Suy ra ${\hat{P}}_1={\hat{M}}_2$ (1)

Mà do Mx// By nên suy ra ${\hat{P}}_1={\hat{M}}_1$ (hai góc so le trong) (2)

Từ (1) và (2) ta suy ra được ${\hat{M}}_1={\hat{M}}_2$.

Xét ΔAMC và ΔHMC có:

$\widehat{MAC}=\widehat{MHC}\left(=90°\right)$

Cạnh MC chung

${\hat{M}}_1={\hat{M}}_2$ (cmt)

Do đó ΔAMC = ΔHMC (cạnh huyền – góc nhọn).

Suy ra AM = HM (hai cạnh tương ứng) (*)

Tam giác MNP cân tại N có NC là đường trung trực đồng thời là đường phân giác xuất phát từ N.

Suy ra ${\hat{N}}_1={\hat{N}}_2$.

Xét ΔHNC và ΔBNC có:

Cạnh CN chung

$\widehat{CHN}=\widehat{CBN}\left(=90°\right)$ (cmt)

Do đó ΔHNC = ΔBNC (cạnh huyền – góc nhọn).

Suy ra NH = NB (hai cạnh tương ứng) (**)

Từ (*) và (**) suy ra: AM + BN = MH + HN = MN (đpcm).

b)

+) Tam giác MAH cân tại M với MC là đường phân giác xuất phát từ đỉnh cân M.

Suy ra MC là đồng thời cũng là đường trung trực của AH.

+) Tam giác NBH cân tại N với NC là đường phân giác xuất phát từ đỉnh cân N.

Suy ra NC đồng thời cũng là đường trung trực của BH.

c) Xét tam giác HAB có CA = CB nên HC là đường trung tuyến của tam giác HAB.

Ta có ΔAMC = ΔHMC (cmt)

Suy ra AC = HC (hai cạnh tương ứng)

Vậy suy ra HC = CA = CB.

Vì đường trung tuyến ứng với cạnh AB và bằng nửa cạnh AB.

Vậy nên tam giác HAB vuông tại H (đpcm).