Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC

Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC sao cho CD = 12 cm. Tính độ dài AD.

Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều

Bài 38 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC sao cho CD = 12 cm. Tính độ dài AD.

Lời giải:

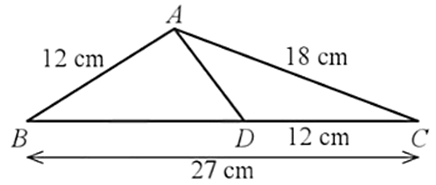
Ta có: $\frac{AC}{DC}=\frac{18}{12}=\frac{3}{2}; \frac{CB}{CA}=\frac{27}{18}=\frac{3}{2}$.

Suy ra $\frac{AC}{DC}=\frac{CB}{CA}=\frac{3}{2}.$

Xét ∆ACB và ∆DCA có:

$\frac{AC}{DC}=\frac{CB}{CA}$ và $\widehat{ACB}$ là góc chung

Suy ra ∆ACB ᔕ ∆DCA (c.g.c).

Do đó $\frac{AC}{DC}=\frac{AB}{DA}$ (tỉ số đồng dạng)

Hay $\frac{18}{12}=\frac{12}{AD}$ nên $AD=\frac{12\cdot 12}{18}=8$ (cm).

Vậy AD = 8 cm.

Lời giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay khác:

• Bài 37 trang 75 SBT Toán 8 Tập 2: Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng: ....

• Bài 39 trang 75 SBT Toán 8 Tập 2: Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD. Kẻ một đường thẳng tuỳ ý đi qua O và cắt cạnh AB tại M, CD tại N ....

• Bài 40 trang 75 SBT Toán 8 Tập 2: Hình 38 cho biết tam giác ABC vuông ở A, AB = 5 cm, AC = 12 cm. Tam giác HAB vuông cân tại H, tam giác KAC vuông cân tại K ....

• Bài 41 trang 75, 76 SBT Toán 8 Tập 2: Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, $\widehat{ABD}=90°$. Hai đường chéo AC và BD cắt nhau tại G ....

• Bài 42* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB. Chứng minh: $\widehat{ADC}+\widehat{ABC}=45°$ ....

• Bài 43* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 2 cm, AC = 3 cm, BC = 4 cm. Chứng minh: $\widehat{BAC}=\widehat{ABC}+2\widehat{BCA}$ ....