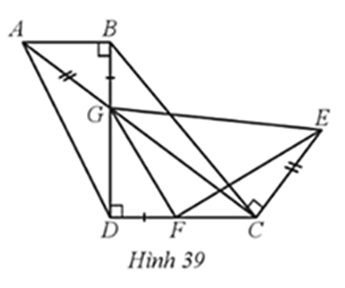
Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, góc ABD = 90 độ
Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 41 trang 75, 76 SBT Toán 8 Tập 2: Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, . Hai đường chéo AC và BD cắt nhau tại G. Điểm E nằm trên đường vuông góc với AC tại C thỏa mãn CE = AG và đoạn thẳng GE không cắt đường thẳng CD. Điểm F nằm trên đoạn thẳng DC và DF = GB. Chứng minh:
a) ∆FDG ᔕ ∆ECG;
b) ∆GDC ᔕ ∆GFE;
c)
Lời giải:
a) Xét ∆GDC với AB // CD, ta có (hệ quả của định lí Thalès)
Do đó
Mặt khác AG = CE, BG = DF nên
Xét ∆FDG và ∆ECG có:
và
Suy ra ∆FDG ᔕ ∆ECG (c.g.c).
b) Vì ∆FDG ᔕ ∆ECG (câu a) nên (hai góc tương ứng) và (tỉ số đồng dạng)
Từ ta có hay
Từ ta có
Xét ∆GDC và ∆GFE có:
và (chứng minh trên)
Suy ra ∆GDC ᔕ ∆GFE (c.g.c).
c) Vì ∆GDC ᔕ ∆GFE (câu b) nên (hai góc tương ứng)
Mà nên
Lời giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay khác: