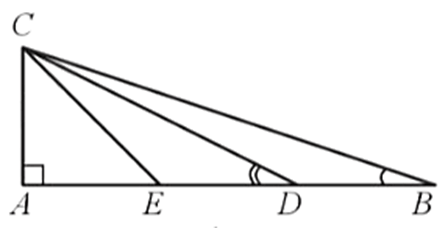
Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB

Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB. Chứng minh: .

Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều

Bài 42* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC vuông ở A có AB = 3AC và điểm D thuộc cạnh AB sao cho AD = 2DB. Chứng minh: $\widehat{ADC}+\widehat{ABC}=45°$.

Lời giải:

Gọi E là trung điểm của AD nên AD = 2AE, AE = ED.

Mà AD = 2DB (giả thiết)

Suy ra AE = ED = DB

Do đó AB = AE + ED + BD = 3AE

Mà AB = 3AC (giả thiết) nên AE = AC hay AE = ED = DB = AC.

Đặt AE = x (x > 0).

Suy ra AE = ED = DB = AC = x, EB = 2x.

Xét ∆ACE vuông tại A, theo định lí Pythagore, ta có:

CE² = AC² + AE² = x² + x² = 2x²

Suy ra $CE=x\sqrt{2}.$

Ta có: $\frac{ED}{EC}=\frac{x}{x\sqrt{2}}=\frac{1}{\sqrt{2}}$, $\frac{EC}{EB}=\frac{x\sqrt{2}}{2x}=\frac{1}{\sqrt{2}}$ nên $\frac{ED}{EC}=\frac{EC}{EB}$

Xét ∆EDC và ∆ECB có:

$\widehat{CEB}$ là góc chung và $\frac{ED}{EC}=\frac{EC}{EB}$ (chứng minh trên)

Suy ra ∆EDC ᔕ ∆ECB (c.g.c).

Do đó $\widehat{ECD}=\widehat{EBC}$ (hai góc tương ứng)

Vì vậy $\widehat{ADC}+\widehat{ABC}=\widehat{EDC}+\widehat{EBC}=\widehat{EDC}+\widehat{ECD}$

Mặt khác, $\widehat{AEC}$ là góc ngoài tại đỉnh E của ∆CED nên $\widehat{AEC}=\widehat{EDC}+\widehat{ECD}$

Do đó $\widehat{ADC}+\widehat{ABC}=\widehat{AEC}.$

Lại có, do ∆AEC là tam giác vuông cân tại A nên $\widehat{AEC}=45°$

Vậy $\widehat{ADC}+\widehat{ABC}=45°$.

Lời giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay khác:

• Bài 37 trang 75 SBT Toán 8 Tập 2: Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng: ....

• Bài 38 trang 75 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12 cm, AC = 18 cm, BC = 27 cm. Điểm D thuộc cạnh BC sao cho CD = 12 cm. Tính độ dài AD ....

• Bài 39 trang 75 SBT Toán 8 Tập 2: Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD. Kẻ một đường thẳng tuỳ ý đi qua O và cắt cạnh AB tại M, CD tại N ....

• Bài 40 trang 75 SBT Toán 8 Tập 2: Hình 38 cho biết tam giác ABC vuông ở A, AB = 5 cm, AC = 12 cm. Tam giác HAB vuông cân tại H, tam giác KAC vuông cân tại K ....

• Bài 41 trang 75, 76 SBT Toán 8 Tập 2: Hình thang ABCD ở Hình 39 có AB // CD, AB < CD, $\widehat{ABD}=90°$. Hai đường chéo AC và BD cắt nhau tại G ....

• Bài 43* trang 76 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 2 cm, AC = 3 cm, BC = 4 cm. Chứng minh: $\widehat{BAC}=\widehat{ABC}+2\widehat{BCA}$ ....