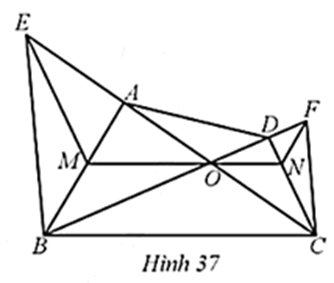
Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD
Trong , cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD. Kẻ một đường thẳng tuỳ ý đi qua O và cắt cạnh AB tại M, CD tại N. Đường thẳng qua M song song với CD cắt AC tại E và đường thẳng qua N song song với AB cắt BD tại F. Chứng minh:
Giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 39 trang 75 SBT Toán 8 Tập 2: Trong Hình 37, cho O là giao điểm hai đường chéo AC và BD của tứ giác ABCD. Kẻ một đường thẳng tuỳ ý đi qua O và cắt cạnh AB tại M, CD tại N. Đường thẳng qua M song song với CD cắt AC tại E và đường thẳng qua N song song với AB cắt BD tại F. Chứng minh:
a) ∆OBE ᔕ ∆OFC;
b) BE // CF.
Lời giải:
a) Do NF // AB, mà M ∈ AB nên NF // MB.
Xét ∆OBM với NF // MB, ta có (hệ quả của định lí Thalès) (1).
Do ME // CD, mà N ∈ CD nên ME // NC.
Xét ∆OEM với ME // NC, ta có (hệ quả của định lí Thalès) (2).
Từ (1) và (2) ta có:
Xét ∆OBE và ∆OFC có:
(hai góc đối đỉnh) và (chứng minh trên)
Suy ra ∆OBE ᔕ ∆OFC (c.g.c).
b) Theo câu a, ta có ∆OBE ᔕ ∆OFC nên (hai góc tương ứng)
Mà hai góc và ở vị trí so le trong nên suy ra BE // CF.
Lời giải SBT Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay khác: