Cho hình thang cân ABCD có AB song song CD, góc D = 45 độ
Giải SBT Toán 8 Bài tập cuối chương 5 - Cánh diều
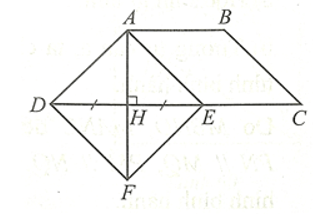
Bài 42 trang 104 SBT Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, . Kẻ AH vuông góc với CD tại H. Lấy điểm E thuộc cạnh CD sao cho HE = DH.
a) Chứng minh tứ giác ABCE là hình bình hành.
b) Đường thẳng qua D và song song với AE cắt AH tại F. Tứ giác ADFE là hình gì? Vì sao?
c*) Tìm điều kiện của hình thang cân ABCD để E là trung điểm của BF (bỏ qua giả thiết ).
Lời giải:
Xét ∆ADH vuông tại H và ∆AEH vuông tại H có:
DH = EH, cạnh AH chung
Do đó ∆ADH = ∆AEH (hai cạnh góc vuông)
Suy ra (hai góc tương ứng)
Hay .
Mà nên .
Lại có nằm ở vị trí đồng vị, suy ra AE // BC.
Tứ giác ABCE có AB // CE, AE // BC nên ABCE là hình bình hành.
b) Do DF // AE nên (hai góc so le trong).
Xét ∆FDH và ∆AEH có:
, , DH = HE
Do đó ∆FDH = ∆AEH (cạnh huyền – góc nhọn)
Suy ra AH = HF (hai cạnh tương ứng)
Hay H là trung điểm của AF
Tứ giác ADFE có hai đường chéo AF và DE vuông góc với nhau tại trung điểm H của mỗi đường nên ADFE là hình thoi.
Tam giác ADE có nên tam giác ADE vuông cân tại A, do đó .
Hình thoi ADFE có nên là hình vuông.
c*) Để E là trung điểm của BF thì BE = FE và ba điểm B, E, F thẳng hàng.
Khi bỏ qua giả thiết thì ta chứng minh được tứ giác ADFE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên ADFE là hình bình hành.
Do ABCE và ADFE đều là hình bình hành nên AE = BC, AE // BC và AE = DF, AE // DF
Suy ra BC = DF và BC // DF
Tứ giác BCFD có BC = DF và BC // DF nên BCFD là hình bình hành.
Mà E là trung điểm của BF, suy ra E là trung điểm của CD hay .
Mặt khác, AB = EC (vì ABCE là hình bình hành), suy ra .
Dễ thấy nếu hình thang cân ABCD (AB // CD) có thì E là trung điểm của BF.
Vậy điều kiện của hình thang cân ABCD (AB // CD) để E là trung điểm của BF là .
Lời giải SBT Toán 8 Bài tập cuối chương 5 hay khác: