Cho hình bình hành ABCD có BC = 2AB Gọi M, N lần lượt
Giải SBT Toán 8 Bài tập cuối chương 5 - Cánh diều
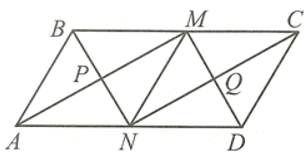
Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có BC = 2AB. Gọi M, N lần lượt là trung điểm của BC, AD.
a) Chứng minh tứ giác MBND là hình bình hành.
b) Gọi P là giao điểm của AM và BN, Q là giao điểm của CN và DM. Chứng minh tứ giác PMQN là hình chữ nhật.
c*) Tìm điều kiện của hình bình hành ABCD để tứ giác PMQN là hình vuông.
d) Tính diện tích của tứ giác PMQN, biết AB = 2 cm, .
Lời giải:
a) Do ABCD là hình bình hành nên BC // AD và BC = AD
Mà M ∈ BC, N ∈ AD nên MB // ND
Lại có M, N lần lượt là trung điểm của BC, AD nên
Do đó MB = MC = NA = ND.
Tứ giác MBND có MB // ND và MB = ND nên là hình bình hành.
b) Tương tự câu a, ta chứng minh được MANC là hình bình hành.
Do MBND, MANC đều là hình bình hành nên PN // MQ, PM // NQ (do P là giao điểm của AM và BN, Q là giao điểm của CN và DM).
Suy ra tứ giác PMQN là hình bình hành.
Xét ∆ABN và ∆MNB có:
AN = BM, (hai góc so le trong do BM // AN), cạnh BN chung
Do đó ∆ABN = ∆MNB (c.g.c). Suy ra AB = MN (hai cạnh tương ứng0
Tứ giác ABMN có AB = BM = MN = AN nên ABMN là hình thoi.
Suy ra AM ⊥ BN, do đó .
Hình bình hành PMQN có nên PMQN là hình chữ nhật.
c*) Để hình chữ nhật PMQN là hình vuông thì PM = PN.
Mà ABMN là hình thoi nên ABMN cũng là hình bình hành.
Suy ra AM, BN cắt nhau tại trung điểm P của mỗi đường.
Mà PM = PN, suy ra AM = BN.
Hình bình hành ABMN có AM = BN nên ABMN là hình chữ nhật.
Suy ra hay .
Hình bình hành ABCD có nên ABCD là hình chữ nhật.
Dễ thấy, nếu hình bình hành ABCD là hình chữ nhật và BC = 2AB thì PMQN là hình vuông.
Vậy điều kiện của hình bình hành ABCD để PMQN là hình vuông là hình bình hành ABCD là hình chữ nhật có BC = 2AB.
d) Ta có BM = AB = 2 cm.
Do ABMN là hình thoi nên AM là tia phân giác của .
Suy ra .
Tam giác ABN có AB = AN và nên tam giác ABN đều.
Suy ra BN = AN = AB = 2 cm.
Do P là trung điểm của BN nên .
Áp dụng định lý Pythagore cho tam giác BMP vuông tại P, ta có: BM2 = BP2 + MP2.
Suy ra MP2 = BM2 ‒ BP2 = 22 ‒ 12 = 3. Do đó .
Do PMQN là hình chữ nhật nên diện tích của PMQN là:
Lời giải SBT Toán 8 Bài tập cuối chương 5 hay khác: