Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD
Giải SBT Toán 8 Bài tập cuối chương 5 - Cánh diều
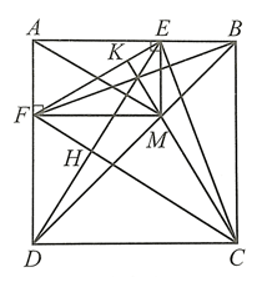
Bài 44 trang 104 SBT Toán 8 Tập 1: Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
a) Chứng minh: DE = CF; DE ⊥ CF.
b*) Chứng minh ba đường thẳng DE, BF, CM cùng đi qua một điểm.
c*) Xác định vị trí của điểm M trên đường chéo BD để diện tích của tứ giác AEMF lớn nhất.
Lời giải:
Gọi H là giao điểm của DE và CF, K là giao điểm của CM và EF.
Do ABCD là hình vuông nên ta có:
a) Do MF ⊥ AD nên tam giác FDM vuông tại F.
Do FM ⊥ AD, DC ⊥ AD nên FM // CD, suy ra > (hai góc so le trong)
Mà (do ABCD là hình vuông nên DM là phân giác góc ADC)
Suy ra , nên ∆FDM cân tại F
Do đó FM = FD.
Do ME ⊥ AB nên
Tứ giác AEMF có nên AEMF là hình chữ nhật.
Suy ra AE = FM.
Do đó AE = FD (vì cùng bằng FM).
Xét ∆ADE vuông tại A và ∆DCF vuông tại D có:
AE = DF, AD = DC (chứng minh trên)
Do đó ∆ADE = ∆DCF (hai cạnh góc vuông)
Suy ra DE = CF (hai cạnh tương ứng) và (hai góc tương ứng)
Xét tam giác ADE vuông tại A, ta có: .
Suy ra hay .
Xét ∆DHF có
Suy ra .
Vậy DE ⊥ CF.
b*) Tương tự câu a, ta chứng minh được BF ⊥ CE.
Xét ∆ABM và ∆CBM có:
AB = BC, , cạnh BM chung
Do đó ∆ABM = ∆CBM (c.g.c)
Suy ra AM = CM (hai cạnh tương ứng)
Mà EF = AM (vì AEMF là hình chữ nhật), suy ra EF = CM.
Xét ∆DEF và ∆FCM có:
DE = FC, EF = CM, DF = FM
Do đó ∆DEF = ∆FCM (c.c.c)
Suy ra (hai góc tương ứng)
Hay .
Trong tam giác HEF vuông tại H, ta có .
Suy ra hay .
Do đó . Do đó CK ⊥ EF.
Trong tam giác CEF, ta có: EH ⊥ CF, FB ⊥ CE, CM ⊥ EF nên ba đường thẳng EH, FB, CM là các đường cao của tam giác CEF.
Hay ba đường thẳng DE, BF, CM là các đường cao của tam giác CEF.
Vậy ba đường thẳng DE, BF, CM cùng đi qua một điểm.
c*) Chu vi của hình chữ nhật AEMF là: 2(AE + AF) = 2(DF + AF) = 2AD.
Mà AD không đồi nên chu vi của hình chữ nhật AEMF không đồi.
Do đó, diện tích của tứ giác AEMF lớn nhất khi AEMF là hình vuông. Suy ra ME = MF.
Khi đó ∆BEM = ∆DFM (cạnh góc vuông – góc nhọn kề).
Suy ra BM = DM hay M là trung điểm của BC.
Vậy với M là trung điểm của BC thì diện tích của tứ giác AEMF lớn nhất.
Lời giải SBT Toán 8 Bài tập cuối chương 5 hay khác: