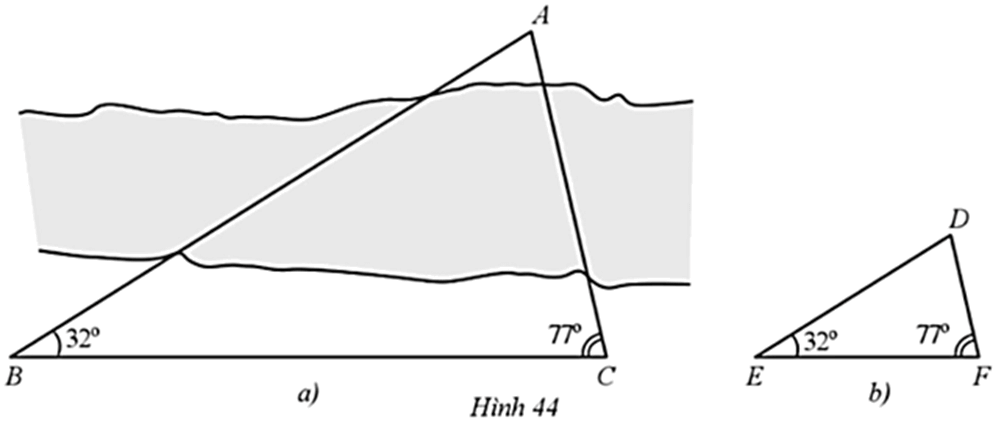
Bác An cần đo khoảng cách AC, với A, C nằm ở hai bên bờ của một hồ nước (Hình 44a)

Bác An cần đo khoảng cách AC, với A, C nằm ở hai bên bờ của một hồ nước (). Bác An đã tiến hành đo như sau:

Giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác - Cánh diều

Bài 46 trang 78 SBT Toán 8 Tập 2: Bác An cần đo khoảng cách AC, với A, C nằm ở hai bên bờ của một hồ nước (Hình 44a). Bác An đã tiến hành đo như sau:

• Chọn điểm B trên bờ (có điểm C) sao cho BC = 20 m;

• Dùng thước đo góc, đo được các góc $\widehat{ABC}=32°, \widehat{ACB}=77°.$

Chứng minh rằng: Nếu thực hiện vẽ trên giấy một tam giác DEF sao cho EF = 10 (cm), $\widehat{DEF}=32°$, $\widehat{DFE}=77°$ (Hình 44b); Đo dộ dài đoạn DF và già sử DF = a (cm) thì độ dài AC mà bác An cần đo là 2a (m).

Lời giải:

Đổi 20 m = 2 000 cm.

Xét ∆ABC và ∆DEF có:

$\widehat{ABC}=\widehat{DEF}=32°$, $\widehat{ACB}=\widehat{DFE}=77°$

Suy ra ∆ABC ᔕ ∆DEF (g.g).

Do đó $\frac{BC}{EF}=\frac{AC}{DF}$ (tỉ số đồng dạng)

Hay $\frac{2 000}{10}=\frac{AC}{a}$ nên AC = 200a (cm) = 2a (m).

Lời giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác hay khác:

• Bài 44 trang 78 SBT Toán 8 Tập 2: Quan sát Hình 43 và chỉ ra hai cặp tam giác đồng dạng: ....

• Bài 45 trang 78 SBT Toán 8 Tập 2: Cho hình thang ABCD có AB // CD, AB = 4 cm, DB = 6 cm và $\widehat{DAB}=\widehat{DBC}.$ Tính độ dài CD ....

• Bài 47 trang 79 SBT Toán 8 Tập 2: Cho tam giác ABC. Lấy E, F, P lần lượt thuộc AB, AC, BC sao cho tứ giác BEFP là hình bình hành (Hình 45). Biết diện tích tam giác AEF và CFP ....

• Bài 48 trang 79 SBT Toán 8 Tập 2: Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB), CF vuông góc với AD (F thuộc đường thẳng AD) ....

• Bài 49 trang 79 SBT Toán 8 Tập 2: Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC, H trên cạnh CD sao cho ....