Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB)
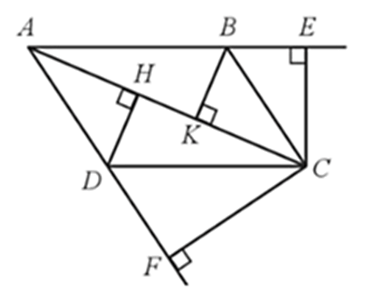
Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB), CF vuông góc với AD (F thuộc đường thẳng AD). Chứng minh: AB.AE + AD.AF = AC.
Giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác - Cánh diều
Bài 48 trang 79 SBT Toán 8 Tập 2: Cho hình bình hành ABCD (AC > BD). Từ C kẻ CE vuông góc với AB (E thuộc đường thẳng AB), CF vuông góc với AD (F thuộc đường thẳng AD). Chứng minh: AB.AE + AD.AF = AC2.
Lời giải:
Gọi H, K lần lượt là hình chiếu của D, B trên đường thẳng AC.
Xét ∆AHD và ∆AFC có:
; là góc chung
Suy ra ∆AHD ᔕ ∆AFC (g.g).
Do đó (tỉ số đồng dạng) hay AD.AF = AC.AH (1).
Xét ∆AKB và ∆AEC có:
; là góc chung
Suy ra ∆AKB ᔕ ∆AEC (g.g).
Suy ra (tỉ số đồng dạng) hay AB.AE = AC.AK (2).
Do ABCD là hình bình hành nên AB = CD, AB // CD.
Suy ra (2 góc ở vị trí so le trong)
Xét ∆ABK và ∆CDH có:
AB = CD,
Suy ra ∆ABK = ∆CDH (cạnh huyền – góc nhọn)
Do đó AK = HC (hai cạnh tương ứng).
Cộng (1) và (2) theo vế ta được:
AD.AF + AB.AE = AC.(AH + AK)
= AC.(AH + HC) (do AK = HC)
= AC.AC = AC2.
Vậy AB.AE + AD.AF = AC2.
Lời giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác hay khác: