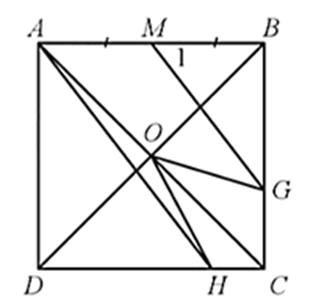
Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC
Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC, H trên cạnh CD sao cho Gọi M là trung điểm của AB. Chứng minh:
Giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác - Cánh diều
Bài 49 trang 79 SBT Toán 8 Tập 2: Cho hình vuông ABCD, gọi O là giao điểm của hai đường chéo, lấy G trên cạnh BC, H trên cạnh CD sao cho Gọi M là trung điểm của AB. Chứng minh:
a) ∆HOD ᔕ ∆OGB;
b) MG // AH.
Lời giải:
a) Do ABCD là hình vuông nên đường chéo là tia phân giác của mỗi góc.
Suy ra
Mặt khác:
Suy ra
Xét ∆HOD và ∆OGB có:
;
Suy ra ∆HOD ᔕ ∆OGB (g.g).
b) Theo câu a, ta có ∆HOD ᔕ ∆OGB, suy ra (tỉ số đồng dạng)
Do đó HD.GB = OB.OD.
Đặt MB = a, khi đó AD = 2a (do M là trung điểm của AB, AB = AD)
Xét ∆ABD vuông tại A, theo định lí Pythagore ta có: BD2 = AB2 + AD2.
Do đó =
Suy ra
Khi đó = =
Vì HD.GB = AD.BM nên
Xét ∆DHA và ∆BMG có:
và
Suy ra ∆DHA ᔕ ∆BMG (c.g.c).
Do đó (hai góc tương ứng)
Mà (hai góc so le trong do AB // CD).
Suy ra
Mà và ở vị trí đồng vị nên MG // AH.
Lời giải SBT Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác hay khác: