Diện tích toàn phần của hình lập phương cạnh a được cho bởi công thức S = 6a^2

Giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) - Cánh diều

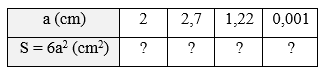
Bài 1 trang 57 SBT Toán 9 Tập 2: Diện tích toàn phần của hình lập phương cạnh a được cho bởi công thức S=6a².

a) Tính các giá trị của S rồi hoàn thiện bảng sau:

b) Tính cạnh a của hình lập phương (theo đơn vị centimét và làm tròn kết quả đến hàng phần trăm), biết diện tích toàn phần của hình lập phương đó bằng 42 cm².

Lời giải:

a) Với a = 2 cm ta có: S = 6.2² = 24 (cm²).

Với a = 2,7 cm ta có: S = 6.(2,7)² = 43,74 (cm²).

Với a = 1,22 cm ta có: S = 6.(1,22)² = 8,9304 (cm²).

Với a = 0, 001 cm ta có: S = 6.(0,001)² = 0,000006 (cm²).

Vậy ta có bảng sau:

b) Ta có: 6a² = 42.

Suy ra a² = 7, nên a ≈ 2,65 cm.

Lời giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) hay khác:

• Bài 2 trang 57 SBT Toán 9 Tập 2: Cho hàm số y=–ax²(a ≠ 0). Tìm a, biết khi x=1,2 thì y=–2,88 ....

• Bài 3 trang 57 SBT Toán 9 Tập 2: Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận ....

• Bài 4 trang 57 SBT Toán 9 Tập 2: Một viên bi lăn trên mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi hàm số ....

• Bài 5 trang 57, 58 SBT Toán 9 Tập 2: a) Điểm A(–0,2; 1) thuộc đồ thị hàm số nào trong các hàm số sau: ....

• Bài 6 trang 58 SBT Toán 9 Tập 2: Cho A là giao điểm của hai đường thẳng y = x – 1 và y = –2x + 8. Chứng minh rằng ....

• Bài 7 trang 58 SBT Toán 9 Tập 2: Cho hàm số y=kx²(k ≠ 0) có đồ thị là một parabol với đỉnh O như Hình 3 ....

• Bài 8 trang 58 SBT Toán 9 Tập 2: Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó ....

• Bài 9 trang 59 SBT Toán 9 Tập 2: Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol ....

• Bài 10 trang 59 SBT Toán 9 Tập 2: a) Vẽ đồ thị các hàm số $\mathrm{y}=-\frac{3}{2}{\mathrm{x}}^2$  và $\mathrm{y}=\frac{3}{2}{\mathrm{x}}^2$  trên cùng một mặt phẳng toạ độ Oxy ....