Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol
Giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) - Cánh diều
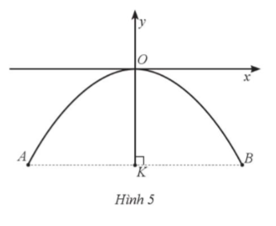
Bài 9 trang 59 SBT Toán 9 Tập 2: Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol với gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Lời giải:
Từ Hình 5, ta có K(0;–4,5).
Gọi hoành độ của điểm B là b (b > 0).
Do tung độ của điểm B bằng tung độ của K nên B(b;–4,5).
Mặt khác, B thuộc parabol nên ta có:
hay b2 = 36, nên b=6 (do b > 0).
Từ đó KB=6 m và AB=2.KB= 2.6 = 12 m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất bằng 12 mét.
Lời giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) hay khác: