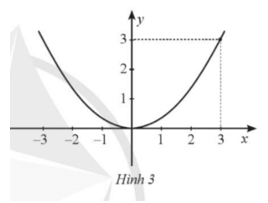
Cho hàm số y = kx^2 (k ≠ 0) có đồ thị là một parabol với đỉnh O như Hình 3

Giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) - Cánh diều

Bài 7 trang 58 SBT Toán 9 Tập 2: Cho hàm số y = kx²(k ≠ 0) có đồ thị là một parabol với đỉnh O như Hình 3.

a) Tìm giá trị của k.

b) Tìm tung độ của điểm thuộc parabol có hoành độ bằng 2.

c) Tìm các điểm thuộc parabol có tung độ bằng 2.

d*) Tìm các điểm (không phải điểm O) thuộc parabol sao cho khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.

Cho hàm số y = kx^2 (k ≠ 0) có đồ thị là một parabol với đỉnh O như Hình 3

Lời giải:

a) Do đồ thị hàm số đi qua A(3; 3) nên 3 = k.3², suy ra $k = \frac{1}{3} .$

Vậy hàm số có dạng $y = \frac{1}{3} x^{2} .$

b) Do tung độ của điểm thuộc parabol có hoành độ bằng 2 nên x = 2.

Thay x = 2 vào hàm số $y = \frac{1}{3} x^{2} .$ ta được: $\frac{1}{3} \cdot 2^{2} = \frac{4}{3} .$

Vậy tung độ của điểm thuộc parabol có hoành độ bằng 2 là y = 2.

c) Do điểm có tung độ bằng 2 nên y = 2.

Thay y = 2 vào hàm số $y = \frac{1}{3} x^{2} .$ ta được:

$\frac{1}{3} \cdot x^{2} = 2,$ suy ra x² = 6, nên $x = \sqrt{6}$ hoặc $x = - \sqrt{6} .$

Vậy các điểm thuộc parabol có tung độ bằng 2 là $(\sqrt{6}; 2)$ và $(- \sqrt{6}; 2) .$

d*) Gọi M(a; b) là điểm thuộc parabol thỏa mãn khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.

Từ đó, ta có: $\frac{1}{3} a^{2} = b (*)$ và |b| = 3.|a|.

Do |b| = 3.|a| nên b = 3a hoặc b = –3a.

– Nếu b = 3a, kết hợp với (*) ta có: $\frac{1}{3} \cdot a^{2} = 3 a$ hay a²= 9a.

Suy ra a(a–9) = 0. Tức là a = 0 hoặc a = 9.

⦁ Với a = 0 thì b = 0, khi đó M(0; 0) (loại vì đây là điểm O).

⦁ Với a = 9 thì b = 27, khi đó M(9; 27).

– Nếu b = –3a, kết hợp với (*) ta có: $\frac{1}{3} \cdot a^{2} = - 3 a$ hay a²= –9a.

Suy ra a(a + 9) = 0. Tức là a = 0 hoặc a = –9.

⦁ Với a = 0 thì b=0, khi đó M(0; 0) (loại vì đây là điểm O).

⦁ Với a = –9 thì b = 27, khi đó M(–9; 27).

Vậy các điểm phải tìm là M(9; 27) và M’(–9; 27).

Lời giải SBT Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) hay khác: