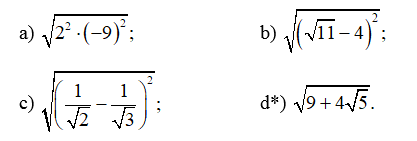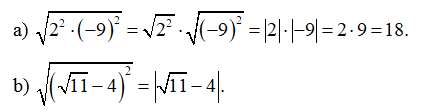Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính

Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:

Giải SBT Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều

Bài 11 trang 57 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:

Lời giải:

Do $\sqrt{11}<\sqrt{16}$ hay $\sqrt{11}<4$ nên $\sqrt{11}-4<0.$

Vì thế, ta có: $\left|\sqrt{11}-4\right|=4-\sqrt{11}.$

Vậy $\sqrt{{\left(\sqrt{11}-4\right)}^2}=\left|\sqrt{11}-4\right|=4-\sqrt{11}.$

c) $\sqrt{{\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}\right)}^2}=\left|\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}\right|=\left|\frac{\sqrt{3}-\sqrt{2}}{\sqrt{2}\cdot \sqrt{3}}\right|=\left|\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}\right|.$

Do 3 > 2 nên $\sqrt{3}>\sqrt{2},$ do đó $\sqrt{3}-\sqrt{2}>0.$

Lại có $\sqrt{6}>0$ nên $\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}>0.$

Vì thế ta có $\left|\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}\right|=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}.$

Vậy $\sqrt{{\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}\right)}^2}=\left|\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}\right|=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}.$

d*) $\sqrt{9+4\sqrt{5}}=\sqrt{2^2+2\cdot 2\cdot \sqrt{5}+{\left(\sqrt{5}\right)}^2}=\sqrt{{\left(2+\sqrt{5}\right)}^2}=\left|2+\sqrt{5}\right|=2+\sqrt{5}.$

Lời giải SBT Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay khác:

• Bài 12 trang 57 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính: a) $\sqrt{\frac{9}{100}\cdot 121};$....

• Bài 13 trang 57 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một thương, hãy tính: a) $\sqrt{\frac{1,21}{0,49}};$....

• Bài 14 trang 57 SBT Toán 9 Tập 1: Rút gọn biểu thức: a) $\sqrt{\frac{{13}^2-{12}^2}{225}};$....

• Bài 15 trang 57 SBT Toán 9 Tập 1: So sánh: a) $\frac{\sqrt{1404}}{\sqrt{351}}$ và $\sqrt{\frac{98}{25}};$....

• Bài 16 trang 58 SBT Toán 9 Tập 1: Sắp xếp $4\sqrt{3};3\sqrt{4};4\sqrt{5};5\sqrt{4};3\sqrt{6}$ theo thứ tự tăng dần....

• Bài 17 trang 58 SBT Toán 9 Tập 1: Cho các biểu thức: $A=\frac{\sqrt{{35}^3+1}}{\sqrt{{35}^2-34}};$ $B=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.$ Chứng minh: A = 6; B = –2.....

• Bài 18 trang 58 SBT Toán 9 Tập 1: Rút gọn biểu thức:a) $\sqrt{20}-\sqrt{45}+\sqrt{5};$....

• Bài 19 trang 58 SBT Toán 9 Tập 1: Cho $a=\sqrt{3-2\sqrt{2}}$ và $b=\sqrt{3+2\sqrt{2}}.$ Chứng minh:....

• Bài 20 trang 58 SBT Toán 9 Tập 1: So sánh: a) $\sqrt{2024}-\sqrt{2023}$ và $\sqrt{2023}-\sqrt{2022};$....

• Bài 21 trang 58 SBT Toán 9 Tập 1: Tốc độ v (m/s) cần có của một vệ tinh để giữ nó chuyển động tròn ổn định trên quỹ đạo với bán kính r (m) quanh Trái Đất được cho bởi công thức ....

• Bài 22 trang 58 SBT Toán 9 Tập 1: Độ dài đường chéo của một hình vuông lớn hơn độ dài cạnh của nó là 4 cm. Tính độ dài cạnh của hình vuông đó.....

• Bài 23 trang 58 SBT Toán 9 Tập 1: Tốc độ v (m/s) của một tàu lượn siêu tốc di chuyển trên một cung tròn bán kính r (m) được cho bởi công thức ...