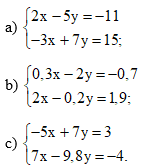Bài 18 trang 20 SBT Toán 9 Tập 1
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
Giải SBT Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn - Cánh diều
Bài 18 trang 20 SBT Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
Lời giải:
a) {2x−5y=−11 (1a)−3x+7y=15 (2a)
Nhân hai vế của phương trình (1a) với 3 và nhân hai vế của phương trình (2a) với 2, ta được hệ phương trình sau: {6x−15y=−33 (3a)−6x+14y=30 (4a)
Cộng từng vế hai phương trình (3a) và (4a), ta nhận được phương trình:
‒y = ‒3 hay y = 3.
Thay y = 3 vào phương trình (1a), ta có: 2x ‒ 5.3 = ‒ 11. (5a)
Giải phương trình (5a):
2x ‒ 5.3 = ‒ 11
2x – 15 = ‒11
2x = ‒11 + 15
2x = 4
x = 2.
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (2; 3).
b) {0,3x−2y=−0,7 (1b)2x−0,2y=1,9 (2b)
Nhân hai vế của phương trình (2b) với 10, ta được hệ phương trình sau: {0,3x−2y=−0,7 (1b)20x−2y=19 (3b)
Trừ từng vế hai phương trình (3b) và (1b), ta nhận được phương trình:
19,7x = 19,7 hay x = 1.
Thay x = 1 vào phương trình (3b), ta được:
20.1 – 2y = 19. (4b)
Giải phương trình (4b):
20.1 – 2y = 19
20 – 2y = 19
–2y = 19 – 20
–2y = –1
y = 0,5.
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (1; 0,5).
c) {−5x+7y=3 (1c)7x−9,8y=−4 (2c)
Nhân hai vế của phương trình (1c) với 7 và nhân hai vế của phương trình (2c) với 5, ta được hệ phương trình sau: {−35x+49y=21 (3c)35x−49y=−20 (4c)
Cộng từng vế hai phương trình (3c) và (4c), ta nhận được phương trình:
0x + 0y = 1.
Phương trình trên vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Lời giải SBT Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn hay khác: