Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A

Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và So sánh các cung nhỏ AB, BC.

Giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

Bài 30 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và $\widehat{BAC}=50°.$ So sánh các cung nhỏ AB, BC.

Lời giải:

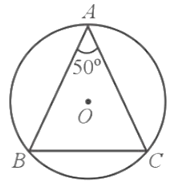
Do tam giác ABC cân tại A nên $\widehat{ABC}=\widehat{ACB}$

Mà $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ (tổng ba góc của tam giác ABC)

Suy ra $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-50°}{2}=65°.$

Ta có: 

⦁ số đo cung nhỏ AB gấp hai lần số đo của góc nội tiếp ACB chắn cung đó nên $\text{sđ}\stackrel{⏜}{AB}=2\cdot \widehat{ACB}=2\cdot 65°=130°.$

⦁ số đo cung nhỏ BC gấp hai lần số đo của góc nội tiếp ABC chắn cung đó nên $\text{sđ}\stackrel{⏜}{BC}=2\cdot \widehat{BAC}=2\cdot 50°=100°.$

Do đó $\text{sđ}\stackrel{⏜}{AB}>\text{sđ}\stackrel{⏜}{BC}.$

Vậy cung nhỏ AB lớn hơn cung nhỏ BC.

Lời giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay khác:

• Bài 27 trang 115 SBT Toán 9 Tập 1: Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao? ....

• Bài 28 trang 115 SBT Toán 9 Tập 1: Nhận định nào sau đây là sai? A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. ....

• Bài 29 trang 115 SBT Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm) ....

• Bài 31 trang 116 SBT Toán 9 Tập 1: Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke.” Bạn Bình đã xác định tâm O của đường tròn như sau: ....

• Bài 32 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M. ....

• Bài 33 trang 116 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’) ....

• Bài 34 trang 116 SBT Toán 9 Tập 1: Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn ....

• Bài 35 trang 117 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD ....

• Bài 36 trang 117 SBT Toán 9 Tập 1: Cho đường tròn (O; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat{ABC}=45°, \widehat{ACB}=15°.$ Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) ....