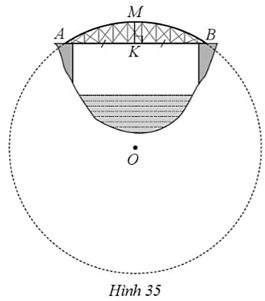
Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m

Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).

Giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

Bài 34 trang 116 SBT Toán 9 Tập 1: Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).

Lời giải:

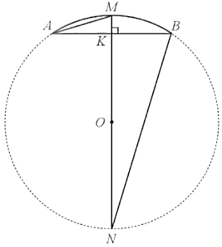
Xét ∆OAB có đồng thời là đường cao của tam giác, hay OK ⊥ AB. Mà MK ⊥ AB nên ba điểm O, K, M thẳng hàng.

Kẻ đường kính MN của đường tròn (O).

Suy ra điểm O thuộc MN và $AK=BK=\frac{AB}{2}=\frac{40}{2}=20 \text{m}.$

Xét ∆AKM và ∆NKB có:

$\widehat{AKM}=\widehat{NKB}=90°;$

$\widehat{MAK}=\widehat{MNB}$ (hai góc nội tiếp cùng chắn cung MB)

Do đó ∆AKM ᔕ ∆NKB (g.g)

Suy ra $\frac{AK}{NK}=\frac{MK}{BK}$ hay $NK=\frac{AK\cdot BK}{MK}=\frac{20\cdot 20}{6}=\frac{200}{3} \text{m}.$

Độ dài đường kính của đường tròn (O) là:

$MN=MK+NK=6+\frac{200}{3}=\frac{218}{3} \text{m}.$

Vậy bán kính của đường tròn chứa cung AMB là

$\frac{218}{3}:2=\frac{109}{3}\approx 36,3 \left(\text{m}\right).$

Lời giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay khác:

• Bài 27 trang 115 SBT Toán 9 Tập 1: Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao? ....

• Bài 28 trang 115 SBT Toán 9 Tập 1: Nhận định nào sau đây là sai? A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. ....

• Bài 29 trang 115 SBT Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm) ....

• Bài 30 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và $\widehat{BAC}=50°.$ So sánh các cung nhỏ AB, BC. ....

• Bài 31 trang 116 SBT Toán 9 Tập 1: Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke.” Bạn Bình đã xác định tâm O của đường tròn như sau: ....

• Bài 32 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M. ....

• Bài 33 trang 116 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’) ....

• Bài 35 trang 117 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD ....

• Bài 36 trang 117 SBT Toán 9 Tập 1: Cho đường tròn (O; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat{ABC}=45°, \widehat{ACB}=15°.$ Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) ....