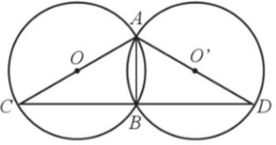
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B, Kẻ đường kính AC của đường tròn (O)

Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). So sánh độ dài dây BC của đường tròn (O) và độ dài dây BD của đường tròn (O’).

Giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

Bài 33 trang 116 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). So sánh độ dài dây BC của đường tròn (O) và độ dài dây BD của đường tròn (O’).

Lời giải:

Trong đường tròn (O), đường kính AC có $\widehat{ABC}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{ABC}=90°.$

Trong đường tròn (O’), đường kính AD có $\widehat{ABD}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{ABD}=90°.$

Xét ∆ABC (vuông tại B) và ABD (vuông tại B) có:

AC = AD = 2R và cạnh AB chung

Do đó ∆ABC = ∆ABD (cạnh huyền – cạnh góc vuông).

Suy ra BC = BD.

Vậy độ dài dây BC của đường tròn (O) bằng độ dài dây BD của đường tròn (O’).

Lời giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay khác:

• Bài 27 trang 115 SBT Toán 9 Tập 1: Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao? ....

• Bài 28 trang 115 SBT Toán 9 Tập 1: Nhận định nào sau đây là sai? A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. ....

• Bài 29 trang 115 SBT Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm) ....

• Bài 30 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và $\widehat{BAC}=50°.$ So sánh các cung nhỏ AB, BC. ....

• Bài 31 trang 116 SBT Toán 9 Tập 1: Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke.” Bạn Bình đã xác định tâm O của đường tròn như sau: ....

• Bài 32 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M. ....

• Bài 34 trang 116 SBT Toán 9 Tập 1: Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn ....

• Bài 35 trang 117 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD ....

• Bài 36 trang 117 SBT Toán 9 Tập 1: Cho đường tròn (O; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat{ABC}=45°, \widehat{ACB}=15°.$ Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) ....