Cho tam giác ABC vuông tại A có đường cao AH, Vẽ đường tròn tâm O đường kính AC

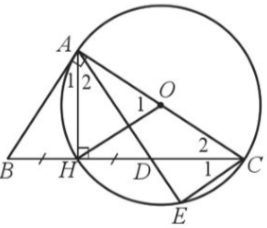
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh:

Giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

Bài 35 trang 117 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh:

a) CH là tia phân giác của góc ACE;

b) OH // EC.

Lời giải:

a) Xét ∆ABH và ∆ADH có:

$\widehat{AHB}=\widehat{AHD}=90°;$

BH = HD (do H là trung điểm của BD);

Cạnh AH chung

Do đó ∆ABH = ∆ADH (hai cạnh góc vuông).

Suy ra $\widehat{A_1}=\widehat{A_2}.$

Mà $\widehat{A_1}=\widehat{C_2}$ (vì cùng phụ với $\widehat{CAH}$) và $\widehat{A_2}=\widehat{C_1}$ (hai góc nội tiếp cùng chắn cung EH)

Suy ra $\widehat{C_1}=\widehat{C_2}.$

Vậy CH là tia phân giác của góc ACE.

b) Xét đường tròn (O) có $\widehat{O_1}$ và $\widehat{C_2}$ lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AH nên $\widehat{O_1}=2\widehat{C_2}$

Mà $\widehat{ACE}=2\widehat{C_2}$ (vì CH là tia phân giác của góc ACE)

Suy ra $\widehat{O_1}=\widehat{ACE},$ mà hai góc này ở vị trí đồng vị

Do đó OH // CE.

Lời giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay khác:

• Bài 27 trang 115 SBT Toán 9 Tập 1: Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao? ....

• Bài 28 trang 115 SBT Toán 9 Tập 1: Nhận định nào sau đây là sai? A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. ....

• Bài 29 trang 115 SBT Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm) ....

• Bài 30 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và $\widehat{BAC}=50°.$ So sánh các cung nhỏ AB, BC. ....

• Bài 31 trang 116 SBT Toán 9 Tập 1: Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke.” Bạn Bình đã xác định tâm O của đường tròn như sau: ....

• Bài 32 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M. ....

• Bài 33 trang 116 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’) ....

• Bài 34 trang 116 SBT Toán 9 Tập 1: Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn ....

• Bài 36 trang 117 SBT Toán 9 Tập 1: Cho đường tròn (O; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat{ABC}=45°, \widehat{ACB}=15°.$ Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) ....