Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn, Vẽ hai tiếp tuyến tại A và B

Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M.

Giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

Bài 32 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (O), hai tiếp tuyến đó cắt nhau tại M.

a) Tính số đo cung nhỏ AB và số đo cung lớn AB nếu $\widehat{AMB}=40°.$

b) Tính diện tích của tứ giác OAMB theo R nếu số đo cung nhỏ AB bằng 120°.

Lời giải:

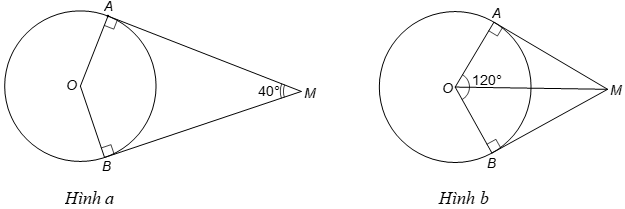
a) (Hình a) Vì MA, MB là các tiếp tuyến của đường tròn (O) nên MA ⊥ OA và MB ⊥ OB.

Xét tứ giác OAMB có: $\widehat{AOM}+\widehat{AMB}+\widehat{OBM}+\widehat{AOB}=360°$

Suy ra $\widehat{AOB}=360°-\widehat{AOM}-\widehat{AMB}-\widehat{OBM}=360°-90°-40°-90°=140°.$

Do đó số đo cung nhỏ AB bằng số đo của góc ở tâm AOB, bằng 140° và số đo cung lớn AB bằng 360° ‒ 140° = 220°.

b) (Hình b) Do số đo cung nhỏ AB bằng 120° suy ra $\widehat{AOB}=120°.$

Lại có MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M nên MA = MB và OM là tia phân giác của góc AOB nên $\widehat{AOM}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 120°=60°.$

Do tam giác OAM vuông tại A nên $MA=OA\cdot \tan \widehat{AOM}=R\sqrt{3}.$

Xét ∆OAM và ∆OBM có: OA = OB; MA = MB; OM là cạnh chung

Do đó ∆OAM = ∆OBM (c.c.c) nên S_∆OAM = S_∆OAM­

Suy ra S_OAMB = S_∆OAM + S_∆OBM­ = 2S_OAM.

Vậy $S_{OAMB}=2\cdot \left(\frac{1}{2}\cdot OA\cdot MA\right)=2\cdot \frac{1}{2}\cdot R\cdot R\sqrt{3}=R^2\sqrt{3}$ (đơn vị diện tích).

Lời giải SBT Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay khác:

• Bài 27 trang 115 SBT Toán 9 Tập 1: Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao? ....

• Bài 28 trang 115 SBT Toán 9 Tập 1: Nhận định nào sau đây là sai? A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm. ....

• Bài 29 trang 115 SBT Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm) ....

• Bài 30 trang 116 SBT Toán 9 Tập 1: Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và $\widehat{BAC}=50°.$ So sánh các cung nhỏ AB, BC. ....

• Bài 31 trang 116 SBT Toán 9 Tập 1: Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke.” Bạn Bình đã xác định tâm O của đường tròn như sau: ....

• Bài 33 trang 116 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’) ....

• Bài 34 trang 116 SBT Toán 9 Tập 1: Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn ....

• Bài 35 trang 117 SBT Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD ....

• Bài 36 trang 117 SBT Toán 9 Tập 1: Cho đường tròn (O; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat{ABC}=45°, \widehat{ACB}=15°.$ Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) ....