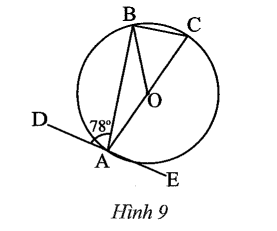
Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O

Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O. Vẽ đoạn thẳng DE tiếp xúc với (O) tại A. Cho biết Tính số đo

Giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

Bài 1 trang 88 sách bài tập Toán 9 Tập 1: Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O. Vẽ đoạn thẳng DE tiếp xúc với (O) tại A. Cho biết $\widehat{BAD}=78°.$ Tính số đo $\widehat{BCA}.$

Lời giải:

Do DE tiếp xúc với (O) tại A, suy ra OA ⊥ DE tại A hay $\widehat{DAO}=90°.$

Suy ra $\widehat{BAO}+\widehat{BAD}=90°$

Nên $\widehat{BAO}=90°-\widehat{BAD}=90°-78°=12°$ hay $\widehat{BAC}=12°.$

Xét ∆ABC có BO là đường trung tuyến và $BO=\frac{1}{2}AC$ nên ∆ABC vuông tại B.

Suy ra: $\widehat{BAC}+\widehat{BCA}=90°$ (tổng hai góc nhọn của tam giác vuông bằng 90°)

Do đó $\widehat{BCA}=90°-\widehat{BAC}=90°-12°=78°.$

Lời giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

• Bài 2 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). ...

• Bài 3 trang 89 sách bài tập Toán 9 Tập 1: Gọi d là khoảng cách từ điểm O đến đường thẳng a. Xác định vị trí tương đối của đường thẳng a và đường tròn (O; r) trong các trường hợp sau...

• Bài 4 trang 89 sách bài tập Toán 9 Tập 1: Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm...

• Bài 5 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D...

• Bài 6 trang 89 sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm....

• Bài 7 trang 89 sách bài tập Toán 9 Tập 1: Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét...