Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B
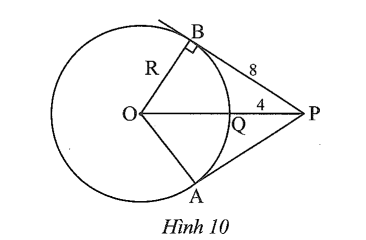
Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo
Giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo
Bài 2 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo
Lời giải:
Do PB và PA là hai tiếp tuyến của đường tròn (O) lần lượt tại B và A
Suy ra OB ⊥ BP; OA ⊥ AP
Nên ∆OBP vuông tại B; ∆OAP vuông tại A.
Xét ∆OPB vuông tại B, ta có OP2 = OB2 + PB2 (định lí Pythagore)
Hay (OQ + QP)2 = OB2 + PB2
Suy ra (R + 4)2 = R2 + 82
R2 + 8R + 16 = R2 + 64
8R = 48
R = 6.
Do đó OP = OQ + QP = 6 + 4 = 10.
Như vậy, suy ra
Theo bài, hai tiếp tuyến AP và BP của đường tròn (O; R) cắt nhau tại P nên OP là tia phân giác của góc AOB.
Khi đó,
Lời giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác: