Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C

❮ Bài trước Bài sau ❯

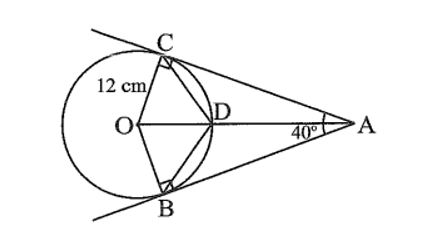
Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D. Cho biết Tính:

Giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

Bài 5 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D. Cho biết BAC^=40°. Tính:

a) Số đo ODC^.

b) Độ dài các đoạn thẳng AC, AB, AO.

(Làm tròn kết quả đến hàng đơn vị của mét.)

Lời giải:

Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C

a) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AO là tia phân giác của BAC^, suy ra OAC^=BAC^2=20°.

Xét ∆OAC vuông tại C có AOC^+OAC^=90°

Suy ra AOC^=90°−OAC^=90°−20°=70° hay DOC^=70°.

Xét ∆ODC cân tại O (do OC = OD), có ODC^=180°−COD^2=180°−70°2=55°.

b) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AC = AB.

Xét ∆OAC vuông tại C ta có:

⦁ AC=OC⋅tanAOC^=12⋅tan70°≈33 ( cm).

Do đó AC = AB ≈ 33 cm.

⦁OC=OA⋅sinOAC^

Suy ra OA=OCsinOAC^=12sin20°≈35 ( cm).

Lời giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

Xem thêm giải sách bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved.