Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm

Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm

Giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

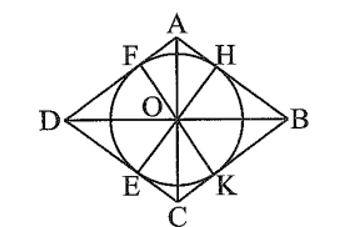
Bài 6 trang 89 sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm

a) Tính độ dài đường cao OH của tam giác AOB.

b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.

c) Tính độ dài các đoạn thẳng AH và BH.

Lời giải:

a) Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc nhau.

Áp dụng định lí Pythagore vào ∆AOB vuông tại O, ta có:

$AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10\text{\hspace{0.17em}\hspace{0.17em}(cm}).$

Ta có $S_{\Delta OAB}=\frac{1}{2}\cdot OA\cdot OB=\frac{1}{2}\cdot OH\cdot AB$

Suy ra OA.OB = OH.AB

Do đó $OH=\frac{OA\cdot OB}{AB}=\frac{6\cdot 8}{10}=4,8 ( \text{cm}).$

b) Lần lượt vẽ các đường cao OK, OE, OF của tam giác BOC, COD, DOA.

Ta có bốn tam giác vuông AOB, AOD, COD, COB bằng nhau (c.g.c), suy ra bốn đường cao OH, OF, OE, OK cũng bằng nhau. Do khoảng cách từ O đến bốn cạnh của hình thoi đều bằng OH nên đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.

c) Xét tam giác OAB vuông tại O có: $\cos \widehat{OAH}=\frac{OA}{AB}.$

Xét tam giác OAH vuông tại H có:

$AH=OA\cdot \cos \widehat{OAB}=OA\cdot \frac{OA}{AB}=\frac{O{A}^2}{AB}=\frac{6^2}{10}=3,6 ( \text{cm}).$

Do đó BH = AB – AH = 10 – 3,6 = 6,4 (cm).

Lời giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

• Bài 1 trang 88 sách bài tập Toán 9 Tập 1: Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O. Vẽ đoạn thẳng DE tiếp xúc với (O) tại A....

• Bài 2 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). ...

• Bài 3 trang 89 sách bài tập Toán 9 Tập 1: Gọi d là khoảng cách từ điểm O đến đường thẳng a. Xác định vị trí tương đối của đường thẳng a và đường tròn (O; r) trong các trường hợp sau...

• Bài 4 trang 89 sách bài tập Toán 9 Tập 1: Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm...

• Bài 5 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D...

• Bài 7 trang 89 sách bài tập Toán 9 Tập 1: Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét...