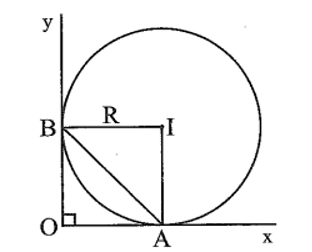
Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B

Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm. Tính R và độ dài AB.

Giải sách bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

Bài 4 trang 89 sách bài tập Toán 9 Tập 1: Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm. Tính R và độ dài AB.

Lời giải:

Ta có Ox và Oy tiếp xúc với (I; R) lần lượt tại A và B

Suy ra IA ⊥ Ox tại A, IB ⊥ Oy tại B và IA = IB = R.

Tứ giác OAIB có ba góc vuông $\left(\widehat{AOB}=\widehat{OAI}=\widehat{OBI}=90°\right)$ và có hai cạnh kề bằng nhau (IA = IB) nên OAIB là hình vuông. Do đó IA = IB = OA = OB = R.

Khi đó, chu vi của hình vuông OAIB là 4R.

Theo bài, chu vi của tứ giác OAIB bằng 20 cm nên 4R = 20, suy ra R = 5 cm.

Xét ∆IAB vuông tại I, theo định lí Pythagore, ta có:

AB² = IA² + IB² = 2R² = 2.5² = 50.

Suy ra $AB=\sqrt{50}=5\sqrt{2} \left(\text{cm}\right).$

Lời giải SBT Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

• Bài 1 trang 88 sách bài tập Toán 9 Tập 1: Cho ba điểm A, B, C cùng nằm trên đường tròn (O) sao cho AC đi qua O. Vẽ đoạn thẳng DE tiếp xúc với (O) tại A....

• Bài 2 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). ...

• Bài 3 trang 89 sách bài tập Toán 9 Tập 1: Gọi d là khoảng cách từ điểm O đến đường thẳng a. Xác định vị trí tương đối của đường thẳng a và đường tròn (O; r) trong các trường hợp sau...

• Bài 5 trang 89 sách bài tập Toán 9 Tập 1: Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D...

• Bài 6 trang 89 sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm....

• Bài 7 trang 89 sách bài tập Toán 9 Tập 1: Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét...