Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân

Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân.

Giải sách bài tập Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo

Bài 2 trang 82 sách bài tập Toán 9 Tập 2: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân.

Lời giải:

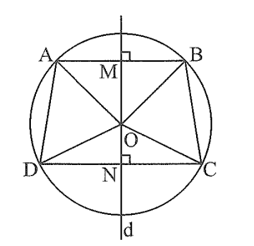
Qua điểm O vẽ đường thẳng d vuông góc với AB tại M và CD tại N.

Ta có OA = OB = OC = OD = R, suy ra đường thẳng d là đường trung trực của AB và CD.

Tam giác AOB cân tại O có OM là đường trung trực nên OM cũng là đường phân giác, suy ra $\hat{A O M} = \hat{B O M} .$

Tương tự, $\hat{D O N} = \hat{C O N} .$

Khi đó, ta có $\hat{A O M} + \hat{A O D} + \hat{D O N} = \hat{B O M} + \hat{B O C} + \hat{C O N} = 180 °$

Suy ra $\hat{A O D} = \hat{B O C} .$

Xét ∆AOD và ∆BOC có:

OA = OB, $\hat{A O D} = \hat{B O C},$ OD = OC.

Do đó ∆AOD = ∆BOC (c.g.c).

Suy ra $\hat{O D A} = \hat{O C B}$ (hai góc tương ứng).

Lại có $\hat{O D C} = \hat{O C D}$ (vì ∆ODC cân tại O do OD = OC).

Khi đó, $\hat{O D A} + \hat{O D C} = \hat{O C B} + \hat{O C D}$ hay $\hat{A D C} = \hat{B C D} .$

Hình thang ABCD có $\hat{A D C} = \hat{B C D}$ nên ABCD là hình thang cân.

Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp hay khác: