Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O)
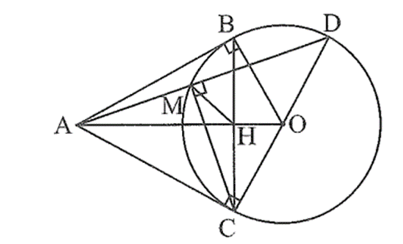
Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là các tiếp điểm). Kẻ đường kính CD của đường tròn (O), đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M. Gọi H là giao điểm của AO và BC. Chứng minh và tứ giác AMHC nội tiếp đường tròn.
Giải sách bài tập Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo
Bài 8 trang 82 sách bài tập Toán 9 Tập 2: Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là các tiếp điểm). Kẻ đường kính CD của đường tròn (O), đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M. Gọi H là giao điểm của AO và BC. Chứng minh và tứ giác AMHC nội tiếp đường tròn.
Lời giải:
⦁ Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau) và OA = OB = R.
Suy ra OA là đường trung trực của đoạn thẳng BC, do đó OA ⊥ BC nên
⦁ Ta có (góc nội tiếp chắn nửa đường tròn (O) đường kính CD), suy ra
Khi đó, tam giác AMC vuông tại M và tam giác AHC vuông tại H cùng nội tiếp đường tròn đường kính AC.
Do đó, tứ giác AMHC nội tiếp đường tròn đường kính AC.
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp hay khác: