Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E

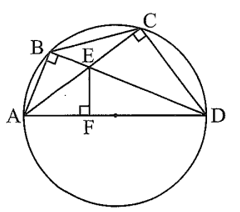
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD tại F. Chứng minh ABEF và DCEF là hai tứ giác nội tiếp.

Giải sách bài tập Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo

Bài 7 trang 82 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD tại F. Chứng minh ABEF và DCEF là hai tứ giác nội tiếp.

Lời giải:

• Ta có $\widehat{ABD}=90°$ (góc nội tiếp chắn nửa đường tròn đường kính AD) hay $\widehat{ABE}=90°.$

Ta cũng có $\widehat{AFE}=90°$ do EF ⊥ AD.

Tam giác ABE vuông tại B và tam giác AFE vuông tại F cùng nội tiếp trong đường tròn đường kính AE.

Do đó, tứ giác ABEF nội tiếp đường tròn đường kính AE.

• Ta có $\widehat{ECD}=\widehat{ACD}=90°$ (góc nội tiếp chắn nửa đường tròn đường kính AD), $\widehat{EFD}=90°$ (do EF ⊥ AD xc).

Tam giác ECD vuông tại C và tam giác EFD vuông tại F cùng nội tiếp trong đường tròn đường kính ED.

Do đó, tứ giác DCEF nội tiếp đường tròn đường kính ED.

Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp hay khác:

• Bài 1 trang 82 sách bài tập Toán 9 Tập 2: Cho MNPQ là tứ giác nội tiếp. Hãy tìm các góc chưa biết của tứ giác MNPQ trong mỗi trường hợp sau:...

• Bài 2 trang 82 sách bài tập Toán 9 Tập 2: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân. ...

• Bài 3 trang 82 sách bài tập Toán 9 Tập 2: Cho hình thoi ABCD có cạnh bằng $a\sqrt{2}$ và nội tiếp đường tròn (O; R). Chứng minh ABCD là hình vuông và tính bán kính R theo a....

• Bài 4 trang 82 sách bài tập Toán 9 Tập 2: Cho nửa đường tròn (O; R) có BC là đường kính. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF, Bx của nửa đường tròn (O) (F là tiếp điểm), ...

• Bài 5 trang 82 sách bài tập Toán 9 Tập 2: Cho đường tròn (O), đường kính AB, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tuỳ ý trên cung nhỏ BM,...

• Bài 6 trang 82 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H...

• Bài 8 trang 82 sách bài tập Toán 9 Tập 2: Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là các tiếp điểm). Kẻ đường kính CD của đường tròn (O), ...