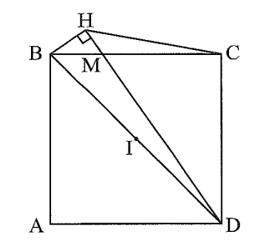
Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C)
Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H. Chứng minh BHCD là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BHCD.
Giải sách bài tập Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo
Bài 6 trang 82 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H. Chứng minh BHCD là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BHCD.
Lời giải:
Ta có (do ABCD là hình vuông), (do BH ⊥ DH).
Khi đó, tam giác BHD vuông tại H và tam giác BCD vuông tại C cùng nội tiếp đường tròn đường kính BD.
Do đó, tứ giác BHCD nội tiếp đường tròn đường kính BD.
Gọi I là trung điểm của BD, khi đó I là tâm của đường tròn ngoại tiếp tứ giác BHCD.
Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp hay khác: