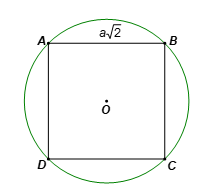
Cho hình thoi ABCD có cạnh bằng a căn bậc hai 2 và nội tiếp đường tròn (O; R). Chứng minh ABCD là hình vuông

Cho hình thoi ABCD có cạnh bằng và nội tiếp đường tròn (O; R). Chứng minh ABCD là hình vuông và tính bán kính R theo a.

Giải sách bài tập Toán 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo

Bài 3 trang 82 sách bài tập Toán 9 Tập 2: Cho hình thoi ABCD có cạnh bằng $a\sqrt{2}$ và nội tiếp đường tròn (O; R). Chứng minh ABCD là hình vuông và tính bán kính R theo a.

Lời giải:

Tứ giác ABCD là hình thoi nên $\widehat{A}=\widehat{C}.$

Tứ giác ABCD nội tiếp đường tròn (O; R) nên $\widehat{A}+\widehat{C}=180°.$

Suy ra $\widehat{A}=\widehat{C}=\frac{180°}{2}=90°.$

Hình thoi ABCD có $\widehat{A}=\widehat{C}=90°$ nên là hình vuông.

Khi đó, hình vuông ABCD nội tiếp trong đường tròn có bán kính là

$R=\frac{AB\sqrt{2}}{2}=\frac{a\sqrt{2}\cdot \sqrt{2}}{2}=a.$

Lời giải SBT Toán 9 Bài 2: Tứ giác nội tiếp hay khác:

• Bài 1 trang 82 sách bài tập Toán 9 Tập 2: Cho MNPQ là tứ giác nội tiếp. Hãy tìm các góc chưa biết của tứ giác MNPQ trong mỗi trường hợp sau:...

• Bài 2 trang 82 sách bài tập Toán 9 Tập 2: Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân. ...

• Bài 4 trang 82 sách bài tập Toán 9 Tập 2: Cho nửa đường tròn (O; R) có BC là đường kính. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF, Bx của nửa đường tròn (O) (F là tiếp điểm), ...

• Bài 5 trang 82 sách bài tập Toán 9 Tập 2: Cho đường tròn (O), đường kính AB, C là trung điểm của OA và dây MN vuông góc với OA tại C. Gọi K là điểm tuỳ ý trên cung nhỏ BM,...

• Bài 6 trang 82 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H...

• Bài 7 trang 82 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD tại F...

• Bài 8 trang 82 sách bài tập Toán 9 Tập 2: Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là các tiếp điểm). Kẻ đường kính CD của đường tròn (O), ...