Quỹ đạo chuyển động của một quả bóng được cho bởi công thức y = 1,5 + x – 0,098x^2, trong đó y (mét) là độ cao của quả bóng

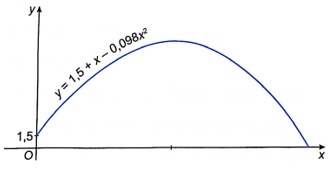
Quỹ đạo chuyển động của một quả bóng được cho bởi công thức y = 1,5 + x – 0,098x, trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất.

Giải sách bài tập Toán 9 Bài 19: Phương trình bậc hai một ẩn - Kết nối tri thức

Bài 6.15 trang 10 sách bài tập Toán 9 Tập 2: Quỹ đạo chuyển động của một quả bóng được cho bởi công thức y = 1,5 + x – 0,098x², trong đó y (mét) là độ cao của quả bóng so với mặt đất và x (mét) là khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí ném (xem hình bên). Tính khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất.

Lời giải:

Theo đề bài, quỹ đạo chuyển động của quả bóng được cho bởi công thức y = 1,5 + x – 0,098x².

Vật chạm đất khi y = 0, khi đó ta có: 1,5 + x – 0,098x² = 0 hay – 0,098x² + x + 1,5 = 0

Ta có: ∆ = 1² – 4 . (–0,098) . 1,5 = 1,588 > 0 nên phương trình có hai nghiệm phân biệt:

$x_1=\frac{-1+\sqrt{\mathrm{1,588}}}{2.\left(-\mathrm{0,098}\right)}\approx -\mathrm{1,33}<0$ (loại)

$x_2=\frac{-1-\sqrt{\mathrm{1,588}}}{2.\left(-\mathrm{0,098}\right)}\approx \mathrm{11,53}>0$ (chọn)

Vậy khoảng cách theo phương ngang từ vị trí ném bóng đến vị trí quả bóng chạm đất xấp xỉ 11,53 m.

Lời giải SBT Toán 9 Bài 19: Phương trình bậc hai một ẩn hay khác:

• Bài 6.9 trang 10 sách bài tập Toán 9 Tập 2: Giải các phương trình sau bằng cách đưa về dạng tích: ...

• Bài 6.10 trang 10 sách bài tập Toán 9 Tập 2: Giải các phương trình sau: (2x + 1)² = 3;    (2 – 3x)² = 5. ...

• Bài 6.11 trang 10 sách bài tập Toán 9 Tập 2: Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình bậc hai sau: ...

• Bài 6.12 trang 10 sách bài tập Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau: ...

• Bài 6.13 trang 10 sách bài tập Toán 9 Tập 2: Tuỳ theo các giá trị của m, hãy giải phương trình ẩn x sau: (2x – 1)² = m. ...

• Bài 6.14 trang 10 sách bài tập Toán 9 Tập 2: Cho phương trình (ẩn x): x² + 4(m + 1)x + 4m² – 3 = 0. ...

• Bài 6.16 trang 11 sách bài tập Toán 9 Tập 2: Công ty sản xuất ván gỗ cần ước tính chiều dài tấm ván (tính bằng feet) có thể tạo ra được từ một khúc gỗ ...