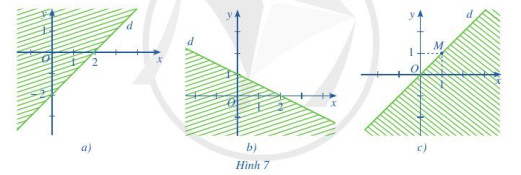
Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Giải Toán lớp 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 3 trang 24 Toán lớp 10 Tập 1: Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Lời giải:

a) Giả sử đường thẳng d: y = ax + b (1) (a ≠ 0)

Quan sát Hình 7a, ta thấy đường thẳng d đi qua hai điểm (0; – 2) và (2; 0).

Thay x = 0, y = – 2 vào (1) ta được: – 2 = b hay b = – 2

Thay x = 2, y = 0 vào (1) ta được: 0 = 2a + b

Suy ra 2a = – b = 2 ⇒ a = 1 (t/m).

Khi đó đường thẳng d: y = x – 2 ⇔ x – y = 2

Xét điểm O(0; 0), ta có: 0 – 0 = 0 < 2

Lại có trên Hình 7a điểm O(0; 0) thuộc phần gạch sọc.

Vậy phần không gạch (không kể d) là miền nghiệm của bất phương trình x – y > 2.

b) Giả sử đường thẳng d: y = ax + b (2) (a ≠ 0)

Quan sát Hình 7b, ta thấy đường thẳng d đi qua 2 điểm (0; 1) và (2; 0).

Thay x = 0, y = 1 vào (2), ta được: b = 1

Thay x = 2, y = 0 vào (2), ta được: 2a + b = 0

Suy ra 2a + 1 = 0 ⇔ a =  $-\frac{1}{2}$(t/m)

Khi đó đường thẳng d: y =  $-\frac{1}{2}x$+ 1 ⇔ x + 2y = 2

Xét điểm O(0; 0). Ta có: 0 + 0 = 0 < 2.

Lại có trên Hình 7b điểm O(0; 0) thuộc phần gạch sọc.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x + 2y > 2.

c) Quan sát Hình 7c, ta thấy đường thẳng d đi qua gốc tọa độ và đi qua điểm M(1; 1).

Do đó phương trình đường thẳng d có dạng: y = ax (a ≠ 0)

Vì d đi qua M nên thay x = 1, y = 1 vào y = ax, ta được: a = 1 (t/m)

Do đó đường thẳng d: y = x ⇔ x – y = 0

Xét điểm (1; 0). Ta có: 1 – 0 = 1 > 0.

Lại có trên Hình 7c điểm (1; 0) nằm trên phần gạch sọc.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x – y < 0.