Cho điểm A(–2; 3) và vecto AM = 3vec i - 2vec j. Vectơ nào trong hình là vecto AM? A. vecto v1; B. vecto v2; C. vecto v3 ; D. vecto v4
Câu hỏi:
Cho điểm A(–2; 3) và \(\overrightarrow {AM} = 3\vec i - 2\vec j\).
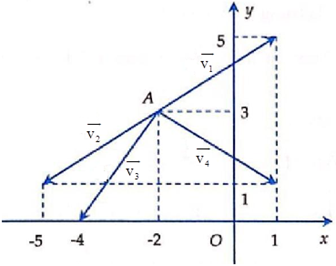
Vectơ nào trong hình là \(\overrightarrow {AM} \)?
A. \[\overrightarrow {{v_1}} \];
B. \[\overrightarrow {{v_2}} \];
C. \[\overrightarrow {{v_3}} \];
D. \(\overrightarrow {{v_4}} \).
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(\overrightarrow {AM} = 3\vec i - 2\vec j\). Suy ra \(\overrightarrow {AM} = \left( {3; - 2} \right)\).
Gọi M(xM; yM). Suy ra \(\overrightarrow {AM} = \left( {{x_M} + 2;{y_M} - 3} \right)\).
Ta có \(\overrightarrow {AM} = \left( {{x_M} + 2;{y_M} - 3} \right) = \left( {3; - 2} \right)\).
Suy ra \(\left\{ \begin{array}{l}{x_M} + 2 = 3\\{y_M} - 3 = - 2\end{array} \right.\)
Khi đó \(\left\{ \begin{array}{l}{x_M} = 1\\{y_M} = 1\end{array} \right.\)
Do đó tọa độ M(1; 1).
Vì vậy \(\overrightarrow {AM} = \overrightarrow {{v_4}} \).
Vậy ta chọn phương án D.
