Cho đường tròn (C): x^2 + y^2 – 4x – 6y + 5 = 0. Đường thẳng d đi qua điểm A(3; 2) và cắt (C) theo một dây cung ngắn nhất có phương trình là: A. 2x – y + 2 = 0; B. x + y – 1 = 0; C. x – y

Hướng dẫn giải

Đáp án đúng là: C

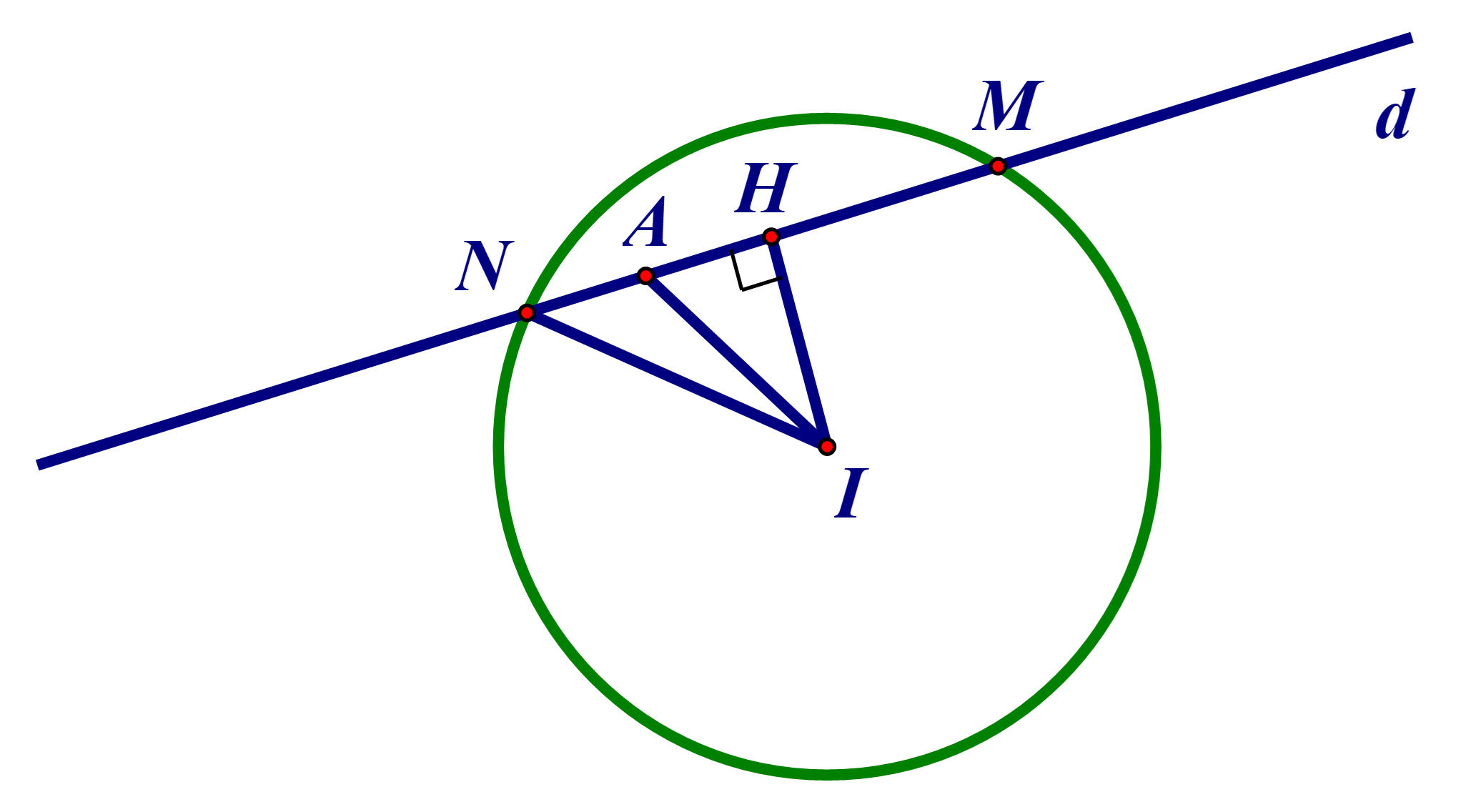
Đường tròn (C) có tâm I(2; 3), bán kính \(R = 2\sqrt 2 \).

Gọi M, N là giao điểm của đường thẳng d và đường tròn (C).

Kẻ IH ⊥ d. Suy ra H là trung điểm MN. Khi đó \(HN = \frac{1}{2}MN\).

∆IHN vuông tại H: IN² = IH² + HN² (Định lí Pytago)

\( \Leftrightarrow {R^2} = I{H^2} + {\left( {\frac{{MN}}{2}} \right)^2}\)

\( \Leftrightarrow {\left( {\frac{{MN}}{2}} \right)^2} = {R^2} - I{H^2}\)

Dây cung MN ngắn nhất khi và chỉ khi IH lớn nhất. Tức là IA ≡ IH hay A ≡ H.

Khi đó IA ⊥ d.

Suy ra d nhận \(\overrightarrow {IA} = \left( {1; - 1} \right)\) làm vectơ pháp tuyến.

Đường thẳng d đi qua A(3; 2) và có vectơ pháp tuyến \(\overrightarrow {IA} = \left( {1; - 1} \right)\).

Suy ra phương trình d: 1(x – 3) – 1(y – 2) = 0

⇔ x – y – 1 = 0.

Vậy ta chọn phương án C.