Cho hệ . Gọi S1 là tập nghiệm của bất phương trình (1), S2 là tập nghiệm của bất
Câu hỏi:
Cho hệ . Gọi S1 là tập nghiệm của bất phương trình (1), S2 là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Trước hết, ta vẽ đường thẳng: (d1): 2x + 3y = 5
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 + 3.0 = 0 < 5, thoả mãn bất phương trình 2x + 3y < 5. Vậy O(0; 0) thuộc miền nghiệm của bất phương trình. Miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch chéo (không kể biên) của (d1).
Vẽ đường thẳng (d2): .
Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có , thoả mãn bất phương trình . Vậy O(0; 0) thuộc miền nghiệm của bất phương trình. Miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch chéo (không kể biên) của (d2).
Miền nghiệm được biểu diễn trong hình dưới đây
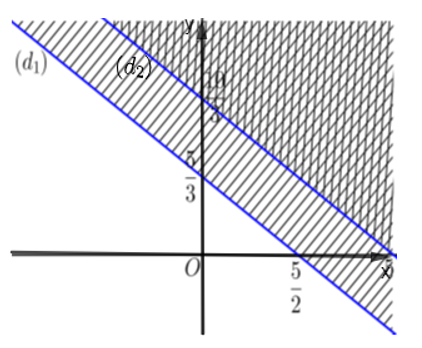
Từ đồ thị biểu diễn miền nghiệm của hệ bất phương trình ta có S1 ⊂ S2; S1 = S; S2 S. Vậy S1 ⊂ S2.

