Giải Toán 10 trang 39 Tập 1 Cánh diều
Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 39 Tập 1 trong Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 39.
Giải Toán 10 trang 39 Tập 1 Cánh diều
Câu hỏi khởi động trang 39 Toán lớp 10 Tập 1: Cầu cảng Sydney là một trong những hình ảnh biểu tượng của thành phố Sydney và nước Australia.
Độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney có thể biểu thị theo độ dài x (m) tính từ chân cầu bên trái dọc theo đường nối với chân cầu bên phải như sau (Hình 10):
y = – 0,00188(x – 251,5)2 + 118.
Hàm số y = – 0,00188(x – 251,5)2 + 118 có gì đặc biệt?
Lời giải:
Để tìm hiểu về hàm số y = – 0,00188(x – 251,5)2 + 118 có gì đặc biệt, chúng ta cùng quan sát Hoạt động 1 trang 39 SGK Toán lớp 10 Tập 1.
Hoạt động 1 trang 39 Toán lớp 10 Tập 1: Cho hàm số y = – 0,00188(x – 251,5)2 + 118
a) Viết công thức xác định hàm số trên về dạng đa thức theo lũy thừa với số mũ giảm dần của x.
b) Bậc của đa thức trên bằng bao nhiêu?
c) Xác định hệ số của x2, hệ số của x và hệ số tự do.
Lời giải:
a) Ta có: y = – 0,00188(x – 251,5)2 + 118
⇔ y = – 0,00188(x2 – 503x + 63252,25) + 118
⇔ y = – 0,00188x2 + 0,94564x – 118,91423 + 118
⇔ y = – 0,00188x2 + 0,94564x – 0,91423
Vậy công thức hàm số được viết về dạng đa thức theo lũy thừa giảm dần của x là
y = – 0,00188x2 + 0,94564x – 0,91423.
b) Đa thức – 0,00188x2 + 0,94564x – 0,91423 có bậc là 2. (bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức)
c) Trong đa thức trên, ta có:
+ Hệ số của x2 là: –0,00188
+ Hệ số của x là: 0,94564
+ Hệ số do là: – 0,91423.
Luyện tập 1 trang 39 Toán lớp 10 Tập 1: Cho hai ví dụ về hàm số bậc hai.
Lời giải:
* Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y = ax2 + bx + c, trong đó a, b, c là những hằng số và a khác 0.
* Ta có thể lấy nhiều ví dụ về hàm số bậc hai, chẳng hạn như hai ví dụ sau:
+ Hàm số y = 10x2 + 3x – 7 là hàm số bậc hai.
+ Hàm số y = – 15x2 + 5 là hàm số bậc hai.
Hoạt động 2 trang 39 Toán lớp 10 Tập 1: Cho hàm số y = x2 + 2x – 3
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
|
x |
– 3 |
– 2 |
– 1 |
0 |
1 |
|
y |
? |
? |
? |
? |
? |
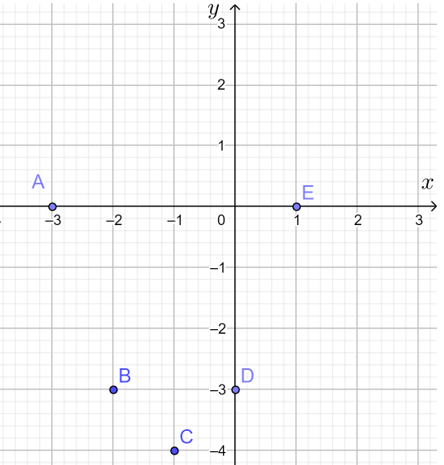
b) Vẽ các điểm A(– 3; 0), B(– 2; – 3), C(– 1; – 4), D(0; – 3), E(1; 0) của đồ thị hàm số y = x2 + 2x – 3 trong mặt phẳng tọa độ Oxy.
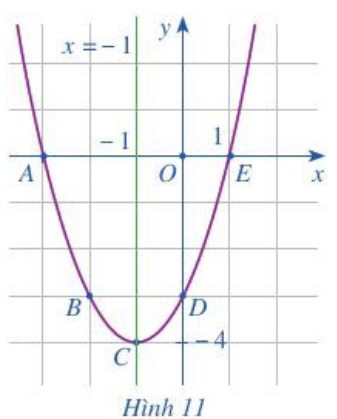
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số y = x2 + 2x – 3 (Hình 11).
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Lời giải:
a) Ta có: y = x2 + 2x – 3.
Với x = – 3 thì y = (– 3)2 + 2 . (– 3) – 3 = 0.
Với x = – 2 thì y = (– 2)2 + 2 . (– 2) – 3 = – 3.
Với x = – 1 thì y = (– 1)2 + 2 . (– 1) – 3 = – 4.
Với x = 0 thì y = 02 + 2 . 0 – 3 = – 3.
Với x = 1 thì y = 12 + 2 . 1 – 3 = 0.
Vậy ta hoàn thành bảng như sau:
|
x |
– 3 |
– 2 |
– 1 |
0 |
1 |
|
y |
0 |
– 3 |
– 4 |
– 3 |
0 |
b) Ta vẽ các điểm lên mặt phẳng tọa độ như sau:
c) Đường cong cần vẽ có dạng:
d) Tọa độ điểm thấp nhất của parabol trên là (– 1; – 4).
Phương trình trục đối xứng của parabol là: x = – 1.
Đồ thị hàm số trên quay bề lõm hướng lên trên.
Lời giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng Cánh diều hay khác: