Giải Toán 10 trang 44 Tập 1 Cánh diều

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 44 Tập 1 trong Bài 3: Dấu của tam thức bậc hai Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 44.

Giải Toán 10 trang 44 Tập 1 Cánh diều

Câu hỏi khởi động trang 44 Toán lớp 10 Tập 1: Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức sau: y = – 200x² + 92 000x – 8 400 000, trong đó x là số sản phẩm được bán ra. Như vậy, việc xác định lãi hay lỗ khi kinh doanh loại sản phẩm trên dẫn tới việc xét dấu của y = – 200x² + 92 000x – 8 400 000, tức là ta cần xét dấu của tam thức bậc hai f(x) = – 200x² + 92 000x – 8 400 000.

Làm thế nào để xét dấu tam thức bậc hai?

Lời giải:

Đa thức bậc hai f(x) = ax² + bx + c (a ≠ 0) được gọi là tam thức tâm bậc hai.

Sau bài học thứ 3 của chương 3 này, ta sẽ biết cách xét dấu tam thức bậc hai và áp dụng vào xét dấu tam thức bậc hai f(x) = – 200x² + 92 000x – 8 400 000.

Ta có: a = – 200, b = 92 000, c = – 8 400 000.

∆ = b² – 4ac = 92000² – 4 . (– 200) . (– 8 400 000) = 1 744 000 000 > 0

$\sqrt{\Delta }=\sqrt{1744000000}=4000\sqrt{109}$

Khi đó f(x) có hai nghiệm $x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-92000+4000\sqrt{109}}{-400}=230-10\sqrt{109}$; $x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-92000-4000\sqrt{109}}{-400}=230+10\sqrt{109}$.

Lại có a = – 200 < 0.

Do đó f(x) < 0 với mọi x thuộc các khoảng $\left(-\infty ;230-10\sqrt{109}\right)$ và $\left(230+10\sqrt{109};+\infty \right)$.

f(x) > 0 với mọi x thuộc khoảng $\left(230-10\sqrt{109};230+10\sqrt{109}\right)$.

Hoạt động 1 trang 44 Toán lớp 10 Tập 1:

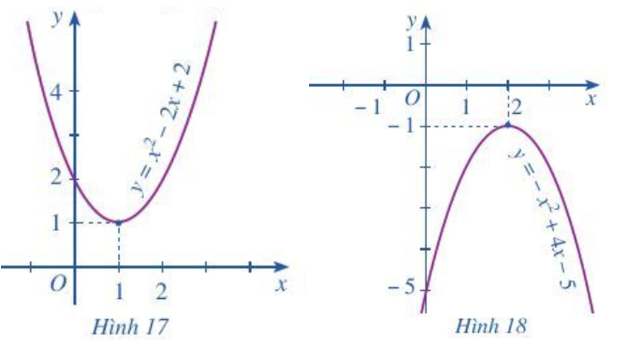
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai f(x) = x² – 2x + 2 trên ℝ. 

b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai f(x) = – x² + 4x – 5 trên ℝ. 

c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0) trên ℝ với dấu của hệ số a trong trường hợp ∆ < 0. 

Lời giải:

a) Quan sát Hình 17 ta thấy parabol nằm hoàn toàn phía trên trục hoành nên tam thức bậc hai f(x) = x² – 2x + 2 > 0 với mọi x ∈ ℝ. 

b) Quan sát Hình 18 ta thấy parabol nằm hoàn toàn phía dưới trục hoành nên tam thức bậc hai f(x) = – x² + 4x – 5 < 0 với mọi x ∈ ℝ. 

c) Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi $x\in ℝ$.

Lời giải bài tập Toán lớp 10 Bài 3: Dấu của tam thức bậc hai Cánh diều hay khác:

• Giải Toán 10 trang 45 Tập 1
• Giải Toán 10 trang 46 Tập 1
• Giải Toán 10 trang 48 Tập 1