Cho hàm số y = x^2 + 2x + 4. Hàm số đạt giá trị nhỏ nhất là bao nhiêu?
Câu hỏi:
Cho hàm số y = x2 + 2x + 4. Hàm số đạt giá trị nhỏ nhất là bao nhiêu?
A. 1
B. 2
C. 3
D. 4
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Hàm số bậc hai y = ax2 + bx + c (với a ≠ 0), khi a > 0, hàm số đạt giá trị nhỏ nhất bằng tại x = .
Ta thấy hàm số y = x2 + 2x + 4 có a = 1 > 0, b = 2, c = 4
Và ∆ = b2 – 4ac = 22 – 4.1.4 = ‒12
Do đó hàm số có giá trị nhỏ nhất bằng = 3 tại x = = 1.
Vậy hàm số đạt giá trị nhỏ nhất là 3 khi x = 1.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Trong các hàm số sau, hàm số nào là hàm số bậc hai?
Xem lời giải »
Câu 2:
Điền vào chỗ trống: Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một ….
Xem lời giải »
Câu 3:
Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?
Xem lời giải »
Câu 4:
Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y =- x2 như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.
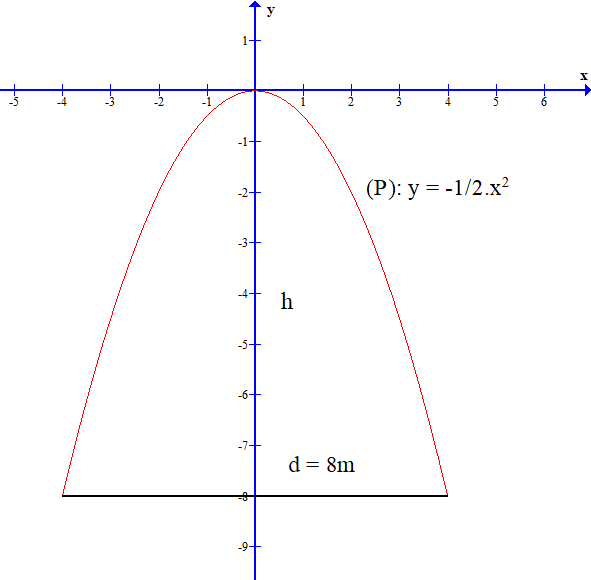
Xem lời giải »
Câu 5:
Cho một vật rơi từ trên cao xuống theo phương thẳng đứng với vận tốc ban đầu là 12 m/s. Hỏi lúc t = 7 s thì vật đã rơi được bao nhiêu mét, biết g = 9,8 m/s2, hệ trục tọa độ chọn mốc từ lúc vật bắt đầu rơi, gốc tọa độ ở vật tại thời điểm bắt đầu rơi.
Xem lời giải »
Câu 6:
Tìm m để đồ thị hàm số y = mx2 + 2(m – 1)x + 1 có trục đối xứng là x = ‒1?
Xem lời giải »


