Để biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 2x + y – 4
Câu hỏi:
Để biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 2x + y – 4 > 0, bạn An đã làm theo 3 bước:
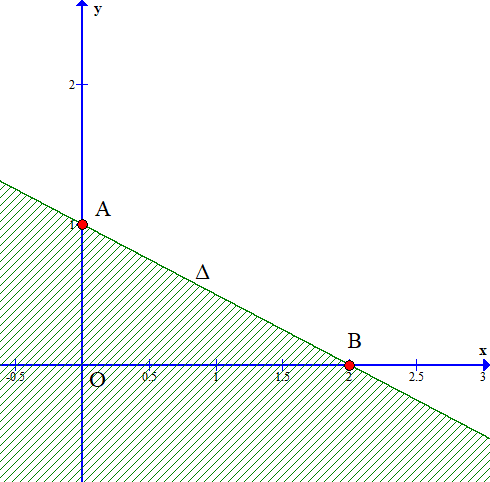
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: 2x + y – 4 = 0.
Bước 2: Lấy một điểm (0; 0) không thuộc ∆. Tính 2. 0 + 0 – 4 = ‒ 4.
Bước 3: Kết luận:
Do ‒4 < 0 nên miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (0; 0).
Bước 4: Biểu diễn miền nghiệm trên trục tọa độ Oxy:
Cô giáo kiểm tra bài bạn An và nói rằng bài bạn làm sai. Bạn An đã làm sai từ bước nào?
A. Bước 1;
B. Bước 2;
C. Bước 3;
D. Bước 4.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Bạn An đã làm sai ở Bước 3: Kết luận:
Do ‒4 < 0 nên miền nghiệm của bất phương trình 2x + y – 4 > 0 là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (0; 0).
