Giải Toán 10 trang 17 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 17 Tập 2 trong Bài 3: Phương trình quy về phương trình bậc hai Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 17.

Giải Toán 10 trang 17 Tập 2 Chân trời sáng tạo

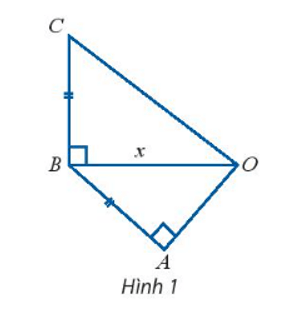
Vận dụng trang 17 Toán lớp 10 Tập 2: Cho tam giác OAB và OBC lần lượt vuông tại A và B như Hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:

a) OC = 3OA;

b) OC = $\frac{5}{4}$OB.

Lời giải:

Ta có OB = x (cm)

Khi đó AB = BC = x – 1 (cm). Do đó x > 1

Xét tam giác OBC vuông tại B, có:

OC² = OB² + BC² (định lí Py – ta – go)

⇔ OC² = x² + (x – 1)² = 2x² – 2x + 1

⇔ OC = $\sqrt{2x^2-2x+1}$

Xét tam giác OAB vuông tại A, có:

OB² = AB² + OA² (định lí Py – ta – go)

⇔ OA² = AB² – OB²

⇔ OA² = x² – (x – 1)² = x² – (x² – 2x + 1) = 2x – 1

⇔ OA = $\sqrt{2x-1}$

a) Vì OC = 3OA nên $\sqrt{2x^2-2x+1}$ = 3$\sqrt{2x-1}$

⇒ 2x² – 2x + 1 = 9(2x – 1)

⇒ 2x² – 2x + 1 = 18x – 9

⇒ 2x² – 20x + 10 = 0

⇒ x² – 10x + 5 = 0

⇒ x = 5 + 2$\sqrt{5}$ hoặc x = 5 – 2$\sqrt{5}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = 5 – 2$\sqrt{5}$ (không thỏa mãn x > 1)

Vậy với x = 5 + 2$\sqrt{5}$ (cm) thì OC = 3OA.

b) Vì OC = $\frac{5}{4}$OB nên $\sqrt{2x^2-2x+1}$ = $\frac{5}{4}$ x

⇒ 2x² – 2x + 1 = $\frac{25}{16}$x²

⇒ 16(2x² – 2x + 1) = 25x²

⇒ 7x² – 32x + 16 = 0

⇒ x = 4 hoặc x = $\frac{4}{7}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = $\frac{4}{7}$(không thỏa mãn x > 1)

Vậy với x = 4 (cm) thì OC = $\frac{5}{4}$OB.

Bài 1 trang 17 Toán lớp 10 Tập 2: Giải phương trình sau:

a) $\sqrt{11x^2-14x-12}=\sqrt{3x^2+4x-7};$

b) $\sqrt{x^2+x-42}=\sqrt{2x-30};$

c) $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5};$

d) $3\sqrt{x^2+x-1}-\sqrt{7x^2+2x-5}=0.$

Lời giải:

a) $\sqrt{11x^2-14x-12}=\sqrt{3x^2+4x-7};$

⇒ 11x² – 14x – 12 = 3x² + 4x – 7

⇒ 8x² – 18x – 5 = 0

⇒ x = $\frac{5}{2}$ hoặc x = $-\frac{1}{4}$

Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy chỉ có x = $\frac{5}{2}$ là thỏa mãn.

Vậy tập nghiệm của phương trình S = .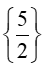

b) $\sqrt{x^2+x-42}=\sqrt{2x-30}$

⇒ x² + x – 42 = 2x – 30

⇒ x² – x – 12 = 0

⇒ x = - 3 hoặc x = 4

Thay lần lượt x = -3 và x = 4 vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.

Vậy tập nghiệm của phương trình S = $\varnothing$ .

c) $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5};$

⇒ 4x² – 4x – 4 = x² + 2x + 5

⇒ 3x² – 6x – 9 = 0

⇒ x = -1 hoặc x = 3

Thay lần lượt các giá trị này vào phương trình đã cho ta thấy x = -1 hoặc x = 3 đều thỏa mãn.

Vậy nghiệm của phương trình là x = -1 và x = 3.

d) $3\sqrt{x^2+x-1}-\sqrt{7x^2+2x-5}=0$

⇔ $3\sqrt{x^2+x-1}=\sqrt{7x^2+2x-5}$

⇒ 9(x² + x – 1) = 7x² + 2x – 5

⇒ 9x² + 9x – 9 = 7x² + 2x – 5

⇒ 2x² + 7x – 4 = 0

⇒ x = -4 và x = $\frac{1}{2}$

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy chỉ có x = -4 thỏa mãn.

Vậy nghiệm của phương trình là x = -4.

Bài 2 trang 17 Toán lớp 10 Tập 2: Giải phương trình sau:

a) $\sqrt{x^2+3x+1}=3;$

b) $\sqrt{x^2-x-4}=x+2;$

c) 2 + $\sqrt{12-2x}$ = x;

d) $\sqrt{2x^2-3x-10}=-5.$

Lời giải:

a) $\sqrt{x^2+3x+1}=3;$

⇒ x² + 3x + 1 = 9

⇒ x² + 3x – 8 = 0

⇒ x = $\frac{-3-\sqrt{41}}{2}$ hoặc x = $\frac{-3+\sqrt{41}}{2}$ .

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy phương trình đã cho có tập nghiệm .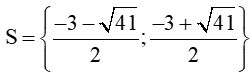

b) $\sqrt{x^2-x-4}=x+2;$

⇒ x² – x – 4 = x² + 4x + 4

⇒ – 5x = 8

⇒ x = $-\frac{8}{5}$

Thay x = $-\frac{8}{5}$ vào phương trình đã cho ta thấy thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = $-\frac{8}{5}$ .

c) 2 + $\sqrt{12-2x}$ = x

⇔ $\sqrt{12-2x}$ = x – 2

⇒ 12 – 2x = x² – 4x + 4

⇒ x² – 2x – 8 = 0

⇒ x = 4 hoặc x = - 2

Thay lần lượt từng giá trị của x vào phương trình đã cho ta thấy chỉ có x = 4 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 4.

d) $\sqrt{2x^2-3x-10}=-5.$

⇒ 2x² – 3x – 10 = 25

⇒ 2x² – 3x – 35 = 0

⇒ x = 5 và x = $-\frac{7}{2}$

Thay lần lượt từng giá trị của x vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

Bài 3 trang 17 Toán lớp 10 Tập 2: Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2cm.

a) Biểu diễn độ dài cạnh huyền BC theo AB.

b) Biết chu vi của tam giác ABC là 24 cm. Tìm độ dài ba cạnh của tam giác đó.

Lời giải:

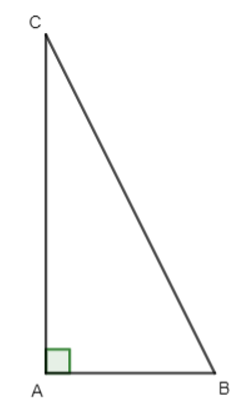
Gọi AB = x (cm) (x > 0)

Vì AB ngắn hơn AC là 2cm nên AC = x + 2 (cm).

a) Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí Py – ta – go)

⇔ BC² = x² + (x + 2)²

⇔ BC² = x² + x² + 4x + 4

⇔ BC² = 2x² + 4x + 4

⇔ BC = $\sqrt{2x^2+4x+4}$ (cm)

Vậy BC = $\sqrt{2x^2+4x+4}$ (cm).

b) Chu vi của tam giác ABC là:

AB + AC + BC = x + x + 2 + $\sqrt{2x^2+4x+4}$ = 2x + 2 + $\sqrt{2x^2+4x+4}$ (cm).

Mà chu vi của tam giác ABC là 24cm nên ta có phương trình:

2x + 2 + $\sqrt{2x^2+4x+4}$ = 24

⇔ $\sqrt{2x^2+4x+4}$ = 22 – 2x

⇒ 2x² + 4x + 4 = 484 – 88x + 4x²

⇒ 2x² – 92x + 480 = 0

⇒ x² – 46x + 240 = 0

⇒ x = 40 và x = 6

Thay lần lượt hai nghiệm vào phương trình đã cho ta thấy x = 6 thỏa mãn.

Với x = 6 thì AB = 6 cm, AC = 6 + 2 = 8 cm, BC = $\sqrt{{2.6}^2+4.6+4}=10$ cm.

Vậy độ dài các cạnh của tam giác ABC lần lượt là AB = 6cm, AC = 8cm, BC = 10 cm.

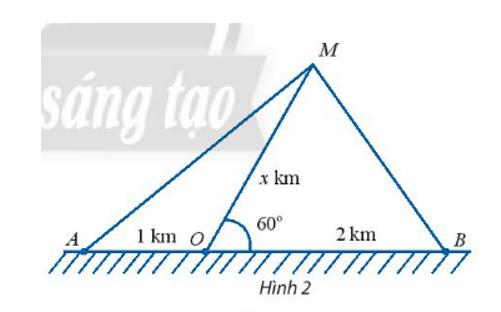
Bài 4 trang 17 Toán lớp 10 Tập 2: Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1km và 2km (Hình 2).

a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.

b) Tìm x để khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A.

c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500m.

Lưu ý: Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Xét tam giác MOB có:

Áp dụng định lí côsin, ta có:

MB² = OM² + OB² – 2.OM.OB.cos$\widehat{BOM}$

⇔ MB² = x² + 2² – 2.x.2.cos60°

⇔ MB² = x² + 4 – 2x

⇔ MB = $\sqrt{x^2-2x+4}$ (km).

Ta lại có:

.

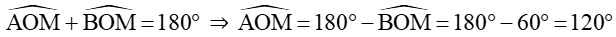
Xét tam giác MOA có:

Áp dụng định lí côsin, ta có:

MA² = OM² + OA² – 2.OM.OA.cos$\widehat{AOM}$

⇔ MA² = x² + 1² – 2.x.1.cos120°

⇔ MA² = x² + 1 + x

⇔ MA = $\sqrt{x^2+x+1}$ (km).

Vậy MA = $\sqrt{x^2+x+1}$ km và MB = $\sqrt{x^2-2x+4}$ km.

b) Để khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A thì

$\sqrt{x^2-2x+4}=\frac{4}{5}\sqrt{x^2+x+1}$

⇒ x² – 2x + 4 = $\frac{16}{25}$ (x² + x + 1)

⇒ 25x² – 50x + 100 = 16x² + 16x + 16

⇒ 9x² – 66x + 84 = 0

⇒ x = $\frac{11-\sqrt{37}}{3}$ hoặc x = $\frac{11+\sqrt{37}}{3}$.

Thay lần lượt các giá trị trên vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy với x = $\frac{11-\sqrt{37}}{3}$ hoặc x = $\frac{11+\sqrt{37}}{3}$ thì khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A.

c) Đổi 500 m = 0,5 km = $\frac{1}{2}$ km

Để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m thì

$\sqrt{x^2-2x+4}=x-\frac{1}{2}$

⇔ x² – 2x + 4 = x² – x + $\frac{1}{4}$

⇔ – x = $-\frac{15}{4}$

⇔ x = $\frac{15}{4}$

Vậy x = $\frac{15}{4}$ thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m.

Lời giải bài tập Toán lớp 10 Bài 3: Phương trình quy về phương trình bậc hai Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 15 Tập 2

• Giải Toán 10 trang 16 Tập 2