Trục đối xứng của parabol y = ‒x^2 + 5x + 3 là đường thẳng có phương trình:

Câu hỏi:

Trục đối xứng của parabol y = ‒x² + 5x + 3 là đường thẳng có phương trình:

A. $x = \frac{5}{4};$

B. $x = - \frac{5}{2};$

C. $x = - \frac{5}{4};$

D. $x = \frac{5}{2} .$

Trả lời:

Hướng dẫn giải

Đáp án đúng là: D

Trục đối xứng của parabol y = ax² + bx + c là đường thẳng $x = - \frac{b}{2 a} .$

Hàm số y = ‒x² + 5x + 3 có hệ số a = ‒1, b = 5, c = 3.

Do đó trục đối xứng của parabol y = ‒x² + 5x + 3 là đường thẳng $x = \frac{- 5}{- 2} = \frac{5}{2} .$

Vậy trục đối xứng của parabol y = ‒x² + 5x + 3 là đường thẳng có phương trình $x = \frac{5}{2} .$

Câu 1:

Tìm tập xác định D của hàm số $y = f (x) = \sqrt{x + 2022} + \frac{1}{x}$

Câu 2:

Tập xác định của hàm số $y = \frac{5 - x}{x^{2} - 2 x}$ là:

Câu 3:

Cho hàm số $f (x) = x + \sqrt{x - 3} .$ Giá trị của f(f(4)) bằng:

Câu 4:

Cho hàm số f(x) = 2x² + ax + b (với a, b là tham số) thoả mãn f(2) = 11, f(3) = ‒7. Giá trị của 5a + 2b bằng:

Câu 5:

Đồ thị dưới đây là của hàm số nào?

Câu 6:

Cho hàm số y = (m – 1)x² – 2(m – 2)x + m – 3 (với m ≠ 1) (P). Đỉnh của (P) là S(‒1; ‒2) thì m có giá trị bằng:

Câu 7:

Hàm số y = ‒x²+ 2x + 3 có đồ thị là hình nào trong các hình sau?

Câu 8:

Cho hàm số y = ax² + bx + c có đồ thị như hình dưới đây.

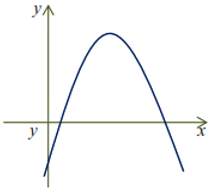
Khẳng định nào sau đây là đúng?

Toán lớp 10 Chân trời sáng tạo