a) Dựa vào đồ thị của hàm số y =1/2x^2 (H.6.2), tìm x sao cho y = 8. b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.
Câu hỏi:
a) Dựa vào đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho y = 8.
b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.
Trả lời:
Hướng dẫn giải
a) Với y = 8, từ điểm 8 trên trục Oy, ta kẻ đường thẳng song song với Ox, đường thẳng này cắt đồ thị hàm số \(y = \frac{1}{2}{x^2}\) tại hai điểm, từ hai điểm đó hạ vuông góc xuống trục Ox, ta thấy hai chân đường vuông góc trên Ox là điểm 4 và – 4.
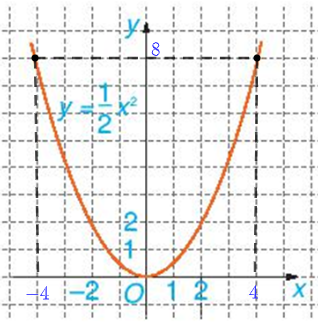
Vậy với y = 8 thì x = 4, x = – 4.
b)
+ Ta có: y = 2x + 1
Tập xác định của hàm số là \(\mathbb{R}\).
Với x = 0 thì y = 2 . 0 + 1 = 1.
Với x = 1 thì y = 2 . 1 + 1 = 3.
Do đó đồ thị hàm số y = 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; 3).
+ Ta có: y = 2x2
Tập xác định của hàm số là \(\mathbb{R}\).
Bảng giá trị tương ứng của x và y
|
x
|
0
|
1
|
– 1
|
2
|
– 2
|
|
y = 2x2
|
0
|
2
|
2
|
8
|
8
|
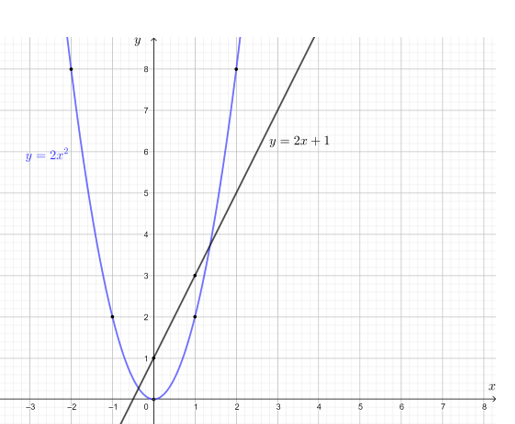
Trên mặt phẳng tọa độ, vẽ đường cong đi qua các điểm (0; 0), (1; 2), (– 1; 2), (2; 8), (– 2; 8), đường cong này chính là đồ thị của hàm số y = 2x2.
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
A. Các câu hỏi trong bài
Quan sát hóa đơn tiền điện ở hình bên. Hãy cho biết tổng lượng điện tiêu thụ trong tháng và số tiền phải trả (chưa tính thuế giá trị gia tăng). Có cách nào mô tả sự phụ thuộc của số tiền phải trả vào tổng lượng điện tiêu thụ hay không?
Xem lời giải »
Câu 2:
Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:
|
Thời điểm (giờ)
|
0
|
4
|
8
|
12
|
16
|
|
Nồng độ bụi PM 2.5 (μg/m3)
|
74,27
|
64,58
|
57,9
|
69,07
|
81,78
|
Bảng 6.1 (Theo moitruongthudo.vn)
a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.
b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?
Xem lời giải »
Câu 3:
Quan sát Hình 6.1.
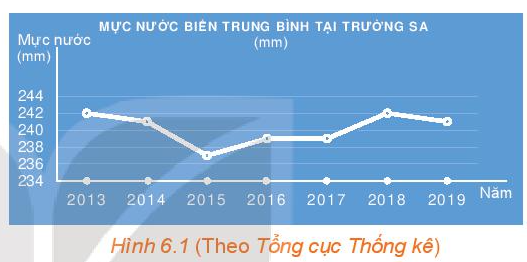
a) Thời gian theo dõi mực nước ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?
Xem lời giải »
Câu 4:
Tính tiền điện
|
Mức điện tiêu thụ
|
Giá bán điện (đồng/kWh)
|
|
Bậc 1 (từ 0 đến 50 kWh)
|
1 678
|
|
Bậc 2 (từ trên 50 đến 100 kWh)
|
1 734
|
|
Bậc 3 (từ trên 100 đến 200 kWh)
|
2 014
|
|
Bậc 4 (từ trên 200 đến 300 kWh)
|
2 536
|
|
Bậc 5 (từ trên 300 đến 400 kWh)
|
2 834
|
|
Bậc 6 (từ trên 400 kWh trở lên)
|
2 927
|
Bảng 6.2
(Theo Tập đoàn Điện lực Việt Nam ngày 20-3-2019)
a) Dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:
|
Lượng điện tiêu thụ (kWh)
|
50
|
100
|
200
|
|
Số tiền (nghìn đồng)
|
?
|
?
|
?
|
Bảng 6.3
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi 0 ≤ x ≤ 50.
Xem lời giải »
Câu 5:
Nếu lượng điện tiêu thụ từ 50 đến 100 kWh (50 < x ≤ 100) thì công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
y = 1,678 . 50 + 1,734(x – 50) = 83,9 + 1,734(x – 50) hay y = 1,734x – 2,8 (nghìn đồng).
Vậy trên tập xác định D = (50; 100], hàm số y mô tả số tiền phải thanh toán có công thức là y = 1,734x – 2,8; tập giá trị của nó là (83,9; 170,6].
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số y = 1,734x – 2,8 trên tập D = (50; 100].
Xem lời giải »
Câu 6:
Cho các hàm số y = – x + 1 và y = x. Tính giá trị y theo giá trị x để hoàn thành bảng sau:
|
x
|
– 2
|
– 1
|
0
|
1
|
2
|
|
y = – x + 1
|
?
|
?
|
?
|
?
|
?
|
|
y = x
|
?
|
?
|
?
|
?
|
?
|
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số y = = – x + 1 và y = x tăng hay giảm?
Xem lời giải »
Câu 7:
Quan sát đồ thị của hàm số y = f(x) = – x2 trên \(\mathbb{R}\)(H.6.5).
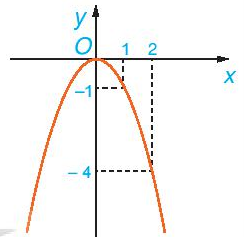
Hình 6.5
Hỏi:
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (– ∞; 0)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng (0; + ∞)?
Xem lời giải »
Câu 8:
Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x2. Hãy cho biết:
a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên \(\mathbb{R}\).
b) Hàm số y = – 2x2 đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).
Xem lời giải »