Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào
Câu hỏi:
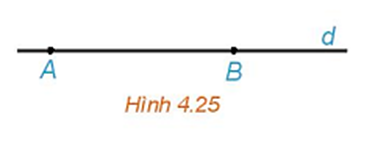
Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?
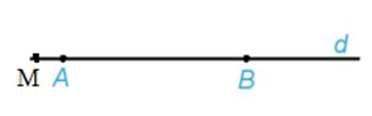
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để .
b) Với điểm M bất kì, ta luôn có:
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t ≤ 0 để
Trả lời:
a) Nếu M thuộc đường thẳng d thì cùng phương
Do đó ta có tồn tại một số thực t thỏa mãn
Nếu tồn tại số t thỏa mãn thì cùng phương hay trùng với .
Do đó A, M, B thẳng hàng hay M thuộc đường thẳng d.
Vì thế khẳng định a) đúng.
b) Nếu M không thuộc đường thẳng d thì và không cùng phương. Do đó
Vì vậy khẳng định b) sai.
c) Nếu điểm M thuộc tia đối của tia AB:
Nếu điểm M thuộc tia đối của tia AB thì hai vectơ và là hai vectơ cùng phương, ngược hướng
Khi đó tồn tại số thực t ≤ 0 thỏa mãn .
Ngược lại, nếu tồn tại số t ≤ 0 để thì hoặc hai vectơ và ngược hướng (với t < 0) hoặc M ≡ A (với t = 0).
Do đó khẳng định c) đúng.
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
Với mỗi cặp vật đặt trên hai đầu của một cánh tay đòn AB, luôn có duy nhất một điểm M thuộc AB để nếu đặt trụ đỡ tại M thì cánh tay đòn ở trạng thái cân bằng (H.4.20). Điều trên còn đúng trong trường hợp tổng quát hơn, chẳng hạn, cánh tay đòn được thay bởi một tấm ván hình đa giác n đỉnh A1, A2, A3, …, An, tại mỗi đỉnh Ai có đặt một vật nặng mi (kg). Ở đây, ta coi cánh tay đòn, tấm ván là không có trọng lượng. Trong Vật lí, điểm M như trên được gọi là điểm khối tâm của hệ chất điểm A1, A2, A3, …, An ứng với các khối lượng m1, m2, m3, …, mn (kg).
Qua bài học này, ta sẽ thấy Hình học cho phép xác định vị trí khối tâm của một hệ chất điểm.
Xem lời giải »
Câu 2:
Cho vecto . Hãy xác định điểm C sao cho
a) Tìm mối quan hệ giữa và
b) Vecto có mối quan hệ như thế nào về hướng và độ dài với vecto
Xem lời giải »
Câu 4:
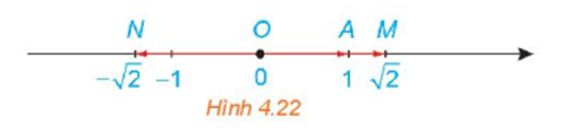
Trên một trục số, gọi O, A, M, N tương ứng biểu diễn các số Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto với vecto . Viết đẳng thức thể hiện mối quan hệ giữa hai vecto và .
Xem lời giải »
Câu 5:
Với và hai số thực k, t, những khẳng định nào sau đây là đúng?
a) Hai vecto và có cùng độ dài bằng
b) Nếu kt ≥ 0 thì cả hai vecto cùng hướng với .
c) Nếu kt < 0 thì cả hai vecto ngược hướng với .
d) Hai vecto và bằng nhau.
Xem lời giải »
Câu 6:
Hãy chỉ ra trên Hình 4.25 hai vecto và . Từ đó, nêu mối quan hệ giữa và .
Xem lời giải »
Câu 7:
Cho tam giác ABC có trọng tâm G. Chứng minh với điểm O tùy ý, ta có:
Xem lời giải »
Câu 8:
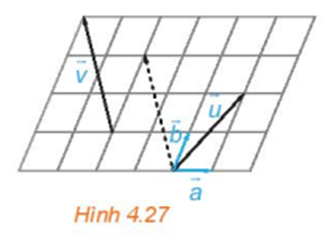
Trong Hình 4.27, hãy biểu thị mỗi vecto theo hai vecto , tức là tìm các số x, y, z, t để
Xem lời giải »